
【题目】已知等差数列{an}中,a1=﹣2,公差d=3;数列{bn}中,Sn为其前n项和,满足:2nSn+1=2n(n∈N+)
(Ⅰ)记An= ![]() ,求数列An的前n项和S;
,求数列An的前n项和S;
(Ⅱ)求证:数列{bn}是等比数列;
(Ⅲ)设数列{cn}满足cn=anbn , Tn为数列{cn}的前n项积,若数列{xn}满足x1=c2﹣c1 , 且xn= ![]() ,求数列{xn}的最大值.
,求数列{xn}的最大值.
【答案】(I)解:∵等差数列{an}中,a1=﹣2,公差d=3,
∴an=﹣2+3(n﹣1)=3n﹣5.
∴An= ![]() =
= ![]() =
= ![]() ,
,
∴数列An的前n项和S= ![]() +
+ ![]() +…+
+…+ ![]()
= ![]()
=﹣ ![]() .
.
(II)证明:由2nSn+1=2n(n∈N+),可得 ![]() .
.
当n=1时,a1=S1= ![]() ;
;
当n≥2时,bn=Sn﹣Sn﹣1= ![]() =
= ![]() .
.
当n=1时也成立.
∴ ![]() =
= ![]() .
.
∴数列{bn}是等比数列,首项为 ![]() ,公比为
,公比为 ![]() .
.
(III)数列{cn}满足cn=anbn= ![]() .
.
数列{xn}满足x1=c2﹣c1= ![]() =
= ![]() .
.
当n≥2时,xn= ![]() =
= ![]() =cn+1﹣cn=
=cn+1﹣cn= ![]() =
= ![]() .
.
当n=1时也成立.
当n≤3时,数列{xn}单调递减;当n≥4时,数列{xn}单调递增,但是xn<0.
∴数列{xn}的最大值是 ![]()
【解析】(I)利用等差数列的通项公式可得an=3n﹣5.利用裂项可得An= ![]() ,利用“裂项求和”可得数列An的前n项和S.(II)由2nSn+1=2n(n∈N+),可得
,利用“裂项求和”可得数列An的前n项和S.(II)由2nSn+1=2n(n∈N+),可得 ![]() .当n=1时,b1=S1=
.当n=1时,b1=S1= ![]() ;当n≥2时,bn=Sn﹣Sn﹣1 . 利用等比数列的通项公式即可证明.(III)数列{cn}满足cn=anbn=
;当n≥2时,bn=Sn﹣Sn﹣1 . 利用等比数列的通项公式即可证明.(III)数列{cn}满足cn=anbn= ![]() .数列{xn}满足x1=c2﹣c1=
.数列{xn}满足x1=c2﹣c1= ![]() .当n≥2时,xn=
.当n≥2时,xn= ![]() =cn+1﹣cn=
=cn+1﹣cn= ![]() .当n≤3时,数列{xn}单调递减;当n≥4时,数列{xn}单调递增,但是xn<0,即可得出.
.当n≤3时,数列{xn}单调递减;当n≥4时,数列{xn}单调递增,但是xn<0,即可得出.
【考点精析】解答此题的关键在于理解等比关系的确定的相关知识,掌握等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系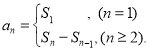 .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】天气预报说,未来三天每天下雨的概率都是0.6,用1、2、3、4表示不下雨,用5、6、7、8、9、0表示下雨,利用计算机生成下列20组随机数,则未来三天恰有两天下雨的概率大约是 .
757 220 582 092 103 000 181 249 414 993
010 732 680 596 761 835 463 521 186 289.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某客运公司用A,B两种型号的车辆承担甲、乙两地间的长途客运业务,每车每天往返一次.A,B两种车辆的载客量分别为36人和60人,从甲地去乙地的营运成本分别为1600元/辆和2400元/辆.公司拟组建一个不超过21辆车的客运车队,并要求B型车不多于A型车7辆.若每天要以不少于900人运完从甲地去乙地的旅客,且使公司从甲地去乙地的营运成本最小,那么应配备A型车、B型车各多少辆?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图.观察图形的信息,回答下列问题. 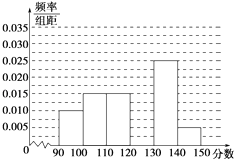
(1)从该校高三模拟考试的成绩中随机抽取一份,利用随机事件频率估计概率,求数学分数恰在[120,130)内的频率;
(2)估计本次考试的中位数;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈[1,2],x2﹣a≥0,命题q:x0∈R,使得x02+(a﹣1)x0﹣1<0,若p∨q为真,p∧q为假,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有五个命题:
①函数y=sin4θ﹣cos4θ的最小正周期是π;
②终边在y轴上的角的集合是 ![]() ;
;
③把 ![]() 的图象向右平移
的图象向右平移 ![]() 得到y=3sin2x的图象;
得到y=3sin2x的图象;
④函数 ![]() 在[0,π]是减函数;
在[0,π]是减函数;
其中真命题的序号是(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( ) 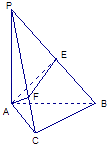
A.2
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100〕后画出如图所示的频率分布直方图.观察图形给出的信息,回答下列问题: 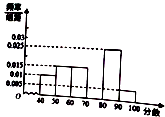
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com