
分析 (Ⅰ)椭圆的一个焦点与抛物线y2=4x的焦点重合,椭圆E上一点到其右焦点F的最短距离为$\sqrt{2}-1$,列出方程组,求出a,b,由此能求出椭圆方程.
(Ⅱ)设A(x1,y1),B(x2,y2),由C(0,1),F(1,0),得kCF=-1,从而kAB=1,设直线l的方程为y=x+m,由$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,得3x2+4mx+2m2-2=0,由此利用根的判别式和韦达定理,结合已知条件能求出直线l的方程.
解答 解:(Ⅰ)∵椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个焦点与抛物线y2=4x的焦点重合,
椭圆E上一点到其右焦点F的最短距离为$\sqrt{2}-1$,
∴$\left\{\begin{array}{l}{c=1}\\{a-c=\sqrt{2}-1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,
解得a=$\sqrt{2}$,b=c=1,
∴椭圆E的方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1.
(Ⅱ)假设存在直线l交椭圆与A、B两点,且F恰好为△ABC的垂心,
设A(x1,y1),B(x2,y2),由C(0,1),F(1,0),得kCF=-1,
∵CF⊥AB,∴kAB=1,
设直线l的方程为y=x+m,由$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,得3x2+4mx+2m2-2=0,
由△>0,得m2<3,且x1+x2=-$\frac{4m}{3}$,x1x2=$\frac{2{m}^{2}-2}{3}$,
由题意,有$\overrightarrow{NP}•\overrightarrow{FQ}$=0,
∵$\overrightarrow{NP}$=(x1,y1-1),$\overrightarrow{FQ}$=(x2-1,y2),
∴x1(x2-1)+y2(y1-1)=0,
即x1(x2-1)+(x2+m)(x1+m-1)=0,
∴2x1x2+(x1+x2)(m-1)+m2-m=0,
∴$2×\frac{2{m}^{2}-2}{3}-\frac{4}{3}m(m-1)+{m}^{2}-m=0$,
解得m=-$\frac{4}{3}$,或m=1,
经检验,当m=1时,△PQN不存在,故舍去m=1,
当m=-$\frac{4}{3}$时,所求直线l存在,且直线l的方程为y=x-$\frac{4}{3}$.
点评 本题考查直线方程的求法,是中档题,解题时要认真审题,注意根的判别式和韦达定理、直线方程,椭圆性质的合理运用.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:选择题
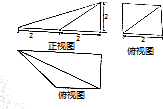
| A. | 2$\sqrt{6}$ | B. | 2$\sqrt{5}$ | C. | 4 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 29-1 | B. | 236 | C. | 210-1 | D. | 245 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 单价x元 | 4 | 5 | 6 | 7 | 8 | 9 |
| 销量y元 | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com