
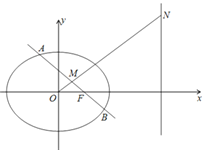
【题目】已知椭圆C1:![]() +
+![]() =1(a>b>0)的右焦点F(1,0),右准线l:x=4.圆C2:x2+y2=b2.A、B为椭圆上不同的两点,AB中点为M.
=1(a>b>0)的右焦点F(1,0),右准线l:x=4.圆C2:x2+y2=b2.A、B为椭圆上不同的两点,AB中点为M.
(1)求椭圆C1的方程;
(2)若直线AB过F点,直线OM交l于N点,求证:NF⊥AB;
(3)若直线AB与圆C2相切,求原点O到AB中垂线的最大距离.
【答案】(1)![]() =1(2)见解析(3)
=1(2)见解析(3)![]()
【解析】
(1)由椭圆的右焦点和右准线得到关于a,b,c的方程组,解方程组即得椭圆的标准方程;(2)设AB:x=my+1,联立直线AB方程和椭圆方程求出点M的坐标和点N的坐标,再计算得kNFkAB=-1,即得NF⊥AB;(3)设AB:x=my+n,求出AB中垂线方程为mx+y-![]() =0,再求出O到AB中垂线的距离,再利用基本不等式求最大距离.
=0,再求出O到AB中垂线的距离,再利用基本不等式求最大距离.
解:(1)椭圆C1:![]() +
+![]() =1(a>b>0)的右焦点F(1,0),右准线l:x=4.
=1(a>b>0)的右焦点F(1,0),右准线l:x=4.
∴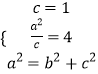 ,
,
解得a=2,b=![]() ,
,
∴椭圆C1的方程为![]() =1.
=1.
(2)由题意,AB的斜率不为0,故设AB:x=my+1,
联立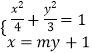 ,得(3m2+4)y2+6my-9=0,
,得(3m2+4)y2+6my-9=0,
由题意得△>0,设A(x1,y1),B(x2,y2),
则y1+y2=-![]() ,y1y2=-
,y1y2=-![]() ,∴M(
,∴M(![]() ),
),
所以OM方程为y=-![]() ,
,
∴N(4,-3m),又F(1,0),∴kNF=-m,
∵kNFkAB=-m![]() =-1,∴NF⊥AB,
=-1,∴NF⊥AB,
当m=0时,NF⊥AB,
综上,NF⊥AB.
(3)C2:x2+y2=3,设AB:x=my+n,
与圆C2相切,得![]() =
=![]() ,
,
与![]() =1联立,得(3m2+4)y2+6mny+3n2-12=0,
=1联立,得(3m2+4)y2+6mny+3n2-12=0,
M(![]() ),
),
所以AB中垂线方程为:y+![]() =-m(x-
=-m(x-![]() ),即mx+y-
),即mx+y-![]() =0,
=0,
所以O到其距离d=![]() =
=![]() ≤
≤![]() =
=![]() ,
,
当3|m|=![]() ,即m=
,即m=![]() 时,取等号.
时,取等号.
综上,点O到AB的中垂线的最大距离为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】大型综艺节目《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方,盲拧在外人看来很神奇,其实原理是十分简单的,要学会盲拧也是很容易的.根据调查显示,是否喜欢盲拧魔方与性别有关.为了验证这个结论,某兴趣小组随机抽取了50名魔方爱好者进行调查,得到的情况如下表所示:
喜欢盲拧 | 不喜欢盲拧 | 总计 | |
男 | 23 | 30 | |
女 | 11 | ||
总计 | 50 |
表(1)
并邀请其中20名男生参加盲拧三阶魔方比赛,其完成情况如下表(2)所示.
成功完成时间(分钟) |
|
|
|
|
人数 | 10 | 4 | 4 | 2 |
表(2)
(Ⅰ)将表(1)补充完整,并判断能否在犯错误的概率不超过0.025的前提下认为是否喜欢盲拧与性别有关?
(Ⅱ)现从表(2)中成功完成时间在![]() 和
和![]() 这两组内的6名男生中任意抽取2人对他们的盲拧情况进行视频记录,求2人成功完成时间恰好在同一组内的概率.
这两组内的6名男生中任意抽取2人对他们的盲拧情况进行视频记录,求2人成功完成时间恰好在同一组内的概率.
附参考公式及参考数据:![]() ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的准线与
的准线与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作圆
作圆![]() 的两条切线,切点为
的两条切线,切点为![]() ,且
,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 是过定点
是过定点![]() 的一条直线,且与抛物线
的一条直线,且与抛物线![]() 交于
交于![]() 两点,过定点
两点,过定点![]() 作
作![]() 的垂线与抛物线交于
的垂线与抛物线交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
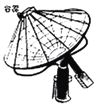
【题目】如图是一种加热食物的太阳灶,上面装有可旋转的抛物面形的反光镜,镜的轴截面是抛物线的一部分,盛食物的容器放在抛物线的焦点处,容器由若干根等长的铁筋焊接在一起的架子支撑.已知镜口圆的直径为8m,镜深1m.
(1)建立适当的坐标系,求抛物线的方程和焦点的位置;
(2)若把盛水和食物的容器近似地看作点,试求每根铁筋的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆市推行“共享吉利博瑞车”服务,租用该车按行驶里程加用车时间收费,标准是“1元/公里![]() 0.2元/分钟”.刚在重庆参加工作的小刘拟租用“共享吉利博瑞车”上下班,同单位的邻居老李告诉他:“上下班往返总路程虽然只有10公里,但偶尔开车上下班总共也需花费大约1小时”,并将自己近50天的往返开车的花费时间情况统计如表:
0.2元/分钟”.刚在重庆参加工作的小刘拟租用“共享吉利博瑞车”上下班,同单位的邻居老李告诉他:“上下班往返总路程虽然只有10公里,但偶尔开车上下班总共也需花费大约1小时”,并将自己近50天的往返开车的花费时间情况统计如表:

将老李统计的各时间段频率视为相应概率,假定往返的路程不变,而且每次路上开车花费时间视为用车时间.
(1)试估计小刘每天平均支付的租车费用(每个时间段以中点时间计算);
(2)小刘认为只要上下班开车总用时不超过45分钟,租用“共享吉利博瑞车”为他该日的“最优选择”,小刘拟租用该车上下班2天,设其中有![]() 天为“最优选择”,求
天为“最优选择”,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前n项和为
的前n项和为![]() ,对于任意的
,对于任意的![]() ,都有
,都有![]() .
.
(1)求![]() ,
,![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)令![]() 问是否存在正数m,使得
问是否存在正数m,使得![]() 对一切正整数n都成立?若存在,求出m的取值范围;若不存在,请说明理由.
对一切正整数n都成立?若存在,求出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某中学举行的物理知识竞赛中,将三个年级参赛学生的成绩在进行整理后分成5组,绘制出如图所示的须率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.

(1)求成绩在50-70分的频率是多少
(2)求这三个年级参赛学生的总人数是多少:
(3)求成绩在80-100分的学生人数是多少
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点
的焦点![]() 为曲线
为曲线![]() 的一个焦点,
的一个焦点, ![]() 为坐标原点,点
为坐标原点,点![]() 为抛物线
为抛物线![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 轴的平行线交抛物线的准线于
轴的平行线交抛物线的准线于![]() ,直线
,直线![]() 交抛物线于点
交抛物线于点![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)若![]() 、
、![]() 、
、![]() 三个点满足
三个点满足![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的导函数f '(x)的图象如图所示,f(-1)=f(2)=3,令g(x)=(x-1)f(x),则不等式g(x)≥3x-3的解集是( )

A. [-1,1]∪[2,+∞)B. (-∞,-1]∪[1,2]
C. (-∞,-1]∪[2,+∞)D. [-1,2]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com