
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=![]() ,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=AD,点M在线段EF上。
,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=AD,点M在线段EF上。
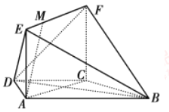
(1)求证:BC⊥平面ACFE;
(2)若![]() ,求证:AM∥平面BDF.
,求证:AM∥平面BDF.
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)由已知梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,易求出AC⊥BC,结合已知中平面ACFE⊥平面ABCD,及平面与平面垂直的性质定理,即可得到BC⊥平面ACFE.
(2)设AC![]() BD=N,则CN:NA=1:2,结合条件可得MF∥AN,且MF=AN,从而得到AM∥NF,由线面平行的判定定理可得结论.
BD=N,则CN:NA=1:2,结合条件可得MF∥AN,且MF=AN,从而得到AM∥NF,由线面平行的判定定理可得结论.
(1)在梯形ABCD中,∵AB∥CD,
AD=CD=CB=a,∠ABC=60°
∴四边形ABCD是等腰梯形
且∠DCA=∠DAC=30°,∠DCB=120°
∴∠ACB=∠DCB-∠DCA=90°
∴AC⊥BC
又∵平面ACFE⊥平面ABCD,交线为AC,
∴BC⊥平面ACFE.
(2)在梯形ABCD中,设AC![]() BD=N,连接FN,则CN:NA=1:2
BD=N,连接FN,则CN:NA=1:2
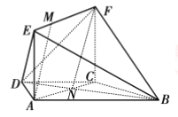
又∵EM:MF=1:2,而EF=AC
∴MF∥AN,且MF=AN
∴四边形ANFM是平行四边形,
∴AM∥NF
又∵NF![]() 平面BDF,AM
平面BDF,AM![]() 平面BDF
平面BDF
∴AM∥平面BDF.


科目:高中数学 来源: 题型:
【题目】给出如下四种说法:
①四个实数![]() 依次成等比数列的必要而不充分条件是
依次成等比数列的必要而不充分条件是![]() .
.
②命题“若![]() 且
且![]() ,则
,则![]() ”为假命题.
”为假命题.
③若![]() 为假命题,则
为假命题,则![]() 均为假命题.
均为假命题.
④若数列![]() 的前项n和
的前项n和![]() ,则该数列的通项公式
,则该数列的通项公式![]() .
.
其中正确说法的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理中是演绎推理的为( )
A. 由金、银、铜、铁可导电,猜想:金属都可导电
B. 猜想数列![]() 的通项公式为
的通项公式为![]()
C. 半径为![]() 的圆的面积
的圆的面积![]() ,则单位圆的面积
,则单位圆的面积![]()
D. 由平面直角坐标系中圆的方程为![]() ,推测空间直角坐标系中球的方程为
,推测空间直角坐标系中球的方程为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
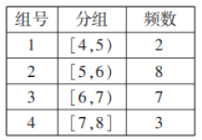
【题目】环境指数是“宜居城市”评比的重要指标.根据以下环境指数的数据,对名列前20名的“宜居城市”的环境指数进行分组统计,结果如表所示,现从环境指数在[4,5)和[7,8]内的“宜居城市”中随机抽取2个市进行调研,则至少有1个市的环境指数在[7,8]的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴,以相同的长度单位建立极坐标系.己知直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,曲线C的极坐标方程为
,曲线C的极坐标方程为![]() .
.
(1)设t为参数,若![]() ,求直线
,求直线![]() 的参数方程和曲线C的直角坐标方程;
的参数方程和曲线C的直角坐标方程;
(2)已知:直线![]() 与曲线C交于A,B两点,设
与曲线C交于A,B两点,设![]() ,且
,且![]() ,
,![]() ,
,![]() 依次成等比数列,求实数a的值.
依次成等比数列,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大提出,坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村真脱贫,坚持扶贫同扶智相结合,帮助贫困村种植蜜柚,并利用电商进行销售,为了更好地销售,现从该村的蜜柚树上随机摘下了100个蜜柚进行测重,其质量分别在![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (单位:克)中,其频率分布直方图如图所示.
(单位:克)中,其频率分布直方图如图所示.

(1)按分层抽样的方法从质量落在![]() ,
, ![]() 的蜜柚中抽取5个,再从这5个蜜柚中随机抽取2个,求这2个蜜柚质量均小于2000克的概率;
的蜜柚中抽取5个,再从这5个蜜柚中随机抽取2个,求这2个蜜柚质量均小于2000克的概率;
(2)以各组数据的中间数代表这组数据的平均水平,以频率代表概率,已知该贫困村的蜜柚树上大约还有5000个蜜柚等待出售,某电商提出两种收购方案:
A.所有蜜柚均以40元/千克收购;
B.低于2250克的蜜柚以60元/个收购,高于或等于2250克的以80元/个收购.
请你通过计算为该村选择收益最好的方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论:
①若点![]() 为角
为角![]() 终边上一点,则
终边上一点,则![]() ;
;
②命题“存在![]() ,
,![]() ”的否定是“对于任意的
”的否定是“对于任意的![]() ,
,![]() ”;
”;
③若函数![]() 在
在![]() 上有零点,则
上有零点,则![]() ;
;
④“![]() (
(![]() 且
且![]() )”是“
)”是“![]() ,
,![]() ”的必要不充分条件.
”的必要不充分条件.
其中正确结论的个数是()
A.0个B.1个C.2个D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com