练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设数列{an}满足：a1＝1，a2＝2，an＋2＝(n≥1，nÎN*)．

    （1）求证：数列{}是常数列；

    （2）求证：当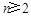时，2＜a－a≤3；

    （3）求a2011的整数部分

     

    【答案】

    略

    【解析】（1）易知，对一切n≥1，an≠0，由an＋2＝，得＝．

    依次利用上述关系式，可得

    ＝＝＝…＝＝＝1，

    从而数列{}是常数列；                      ……………………………4分

    （2）由（1）得an＋1＝an＋．

    又a1＝1，∴可知数列{an}递增，则对一切n≥1，有an≥1成立，

    从而0＜≤1．                                ……………………………6分

    当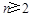时，an2＝(an－1＋)2＝a－1＋＋2，

    于是an2－a－1＝＋2，

    ∴ 2＜a－a≤3；                            ……………………………8分

    （3）当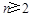时，an2＝a－1＋＋2，

    ∴a＝＋…＋＋a＋2(n－1)．

    a＝1，a＝4，则当n≥3时，

    a＝＋…＋＋a＋2(n－1)＝＋…＋＋1＋1＋2(n－1)

    ＝＋…＋＋2n＞2n．

    a＝＋…＋＋2(2011－1)＋1＞4021＞3969＝632，  ……………………10分

    a＝＋…＋＋2(2011－1)＋1＝4021＋＋…＋

    ＜4020＋＋＋＋…＋＝4022＋(＋＋…＋)

    ＝4022＋[(＋＋…＋)＋(＋＋…＋)＋(＋＋…＋)]

    ＜4022＋[(＋＋…＋)＋(＋＋…＋)＋(＋＋…＋)]

    ＝4022＋(×38＋×160＋…＋×1811)

    ＜4022＋(19＋4＋10)＜4039＜4096＝642．        ……………………14分

    ∴63＜a2011＜64，即a2011的整数部分为63．           ……………………16分

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设数列{an}满足a1=0，an+1=can3+1-c，n∈N*，其中c为实数
    （1）证明：an∈[0，1]对任意n∈N*成立的充分必要条件是c∈[0，1]；
    （2）设0＜c＜
    1
    3
    ，证明：an≥1-（3c）n-1，n∈N*；
    （3）设0＜c＜
    1
    3
    ，证明：
    a
    2
    1
    +
    a
    2
    2
    +…
    a
    2
    n
    ＞n+1-
    2
    1-3c
    ，n∈N*    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f(x)=
    1
    4x+m
    (m＞0)    ，当x1、x2∈R且x1+x2=1时，总有f(x1)+f(x2)=
    1
    2
    ．
    （1）求m的值；
    （2）设数列an满足an=f(
    0
    n
    )+f(
    1
    n
    )+f(
    2
    n
    )+…+f(
    n
    n
    )    ，求an的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设数列{an}满足a1=a，an+1=can+1-c，n∈N*其中a，c为实数，且c≠0
    （Ⅰ）求数列{an}的通项公式
    （Ⅱ）设a=
    1
    2
    ，c=
    1
    2
    ，bn=n（1-an），n∈N*，求数列{bn}的前n项和Sn；
    （Ⅲ）若0＜an＜1对任意n∈N*成立，求实数c的范围．（理科做，文科不做）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设数列{an}满足：a1=
    5
    6
    ，且an=
    1
    3
    an-1+
    1
    3
    （n∈N*，n≥2）
    （1）求证：数列{an-
    1
    2
    }为等比数列，并求数列{an}的通项an；
    （2）求{an}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设n∈N*，不等式组
    x＞0
    y＞0
    y≤-nx+2n
    所表示的平面区域为Dn，把Dn内的整点（横、纵坐标均为整数的点）按其到原点的距离从近到远排列成点列：（x1，y1），（x2，y2），…，（xn，yn）
    （1）求（xn，yn）；
    （2）设数列{an}满足a1=x1，an=
    y
    2
    n
    (
    1
    y
    2
    1
    +
    1
    y
    2
    2
    +…+
    1
    y
    2
    n-1
    )，(n≥2)    ，求证：n≥2时，
    an+1
    (n+1
    )
    2
     
    -
    an
    n
    2
     
    =
    1
    n
    2
     
    ；
    （3）在（2）的条件下，比较(1+
    1
    a1
    )(1+
    1
    a2
    )…(1+
    1
    an
    )    与4的大小．

    查看答案和解析>>

    同步练习册答案