
(本小题满分12分)
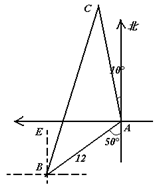
我缉私巡逻艇在一小岛A南偏西50º的方向,距小岛12海里的B处,发现隐藏在小岛边上的一走私船正开始向岛北偏西 10º方向行驶,测得其速度为每小时10海里,问我巡逻艇须用多大的速度朝什么方向航行才能恰在两小时后截获该走私船?(必要时,可参考下列数据sin38º≈0.62,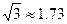 )
)
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
三、解答题:(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.)
16. (本小题满分12分)
已知向量 ,定义函数
,定义函数
(Ⅰ)求函数 最小正周期;
最小正周期;
(Ⅱ)在△ABC中,角A为锐角,且 ,求边AC的长.
,求边AC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
三、解答题(本大题有5道小题,各小题12分,共60分)
17.在 中,
中, 分别是角
分别是角 的对边,向量
的对边,向量 ,
,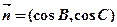 ,且
,且 .
.
(1)求角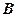 的大小;
的大小;
(2)设 ,且
,且 的最小正周期为
的最小正周期为 ,求
,求 在
在
区间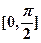 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(8分)如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知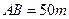 ,
,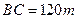 ,于A处测得水深
,于A处测得水深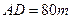 ,于B处测得水深
,于B处测得水深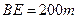 ,于C处测得水深
,于C处测得水深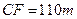 ,求∠DEF的余弦值。
,求∠DEF的余弦值。
 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数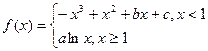
 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点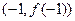 处的切线的斜率是
处的切线的斜率是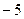 .
.
(Ⅰ)求实数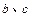 的值;
的值;
(Ⅱ)求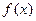 在区间
在区间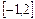 上的最大值;
上的最大值;
(Ⅲ)对任意给定的正实数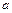 ,曲线
,曲线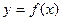 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得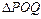 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在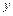 轴上?说明理由。
轴上?说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题共13分)
在△ABC中,a,b,c分别为内角A,B,C的对边,且b2+c2-a2=bc.
(Ⅰ)求角A的大小;
(Ⅱ)设函数 ,当
,当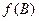 取最大值
取最大值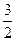 时,判断△ABC的形状.
时,判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
.(本题满分12分)
在 中,
中,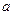 ,
,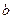 ,
,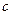 分别为内角
分别为内角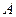 ,
, ,
,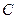 所对的边,且满足
所对的边,且满足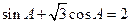 .
.
(Ⅰ)求角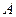 的大小;
的大小;
(Ⅱ)现给出三个条件:①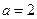 ;②
;②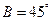 ;③
;③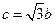 .
.
试从中选出两个可以确定 的条件,写出你的选择,并以此为依据求
的条件,写出你的选择,并以此为依据求 的面积(只需写出一个选定方案即可,选多种方案以第一种方案记分) .
的面积(只需写出一个选定方案即可,选多种方案以第一种方案记分) .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com