
分析 (1)令n=2,由a2>a1,结合条件c∈(0,$\frac{1}{2}$),由二次不等式的解法即可得到;
(2)运用数学归纳法,结合不等式的性质,即可得证;
(3)先证n=1成立;再证当n≥2时,由an+1=can2+1-c,可得an>1-(2c)n-1>0,运用不等式的性质和等比数列的求和公式,即可得证.
解答 解:(1)由an+1=can2+1-c,可得a2=ca12+1-c,
由a2>a1,可得(a1-1)(a1+1-$\frac{1}{c}$)>0,
由c∈(0,$\frac{1}{2}$),可得$\frac{1}{c}$>2,
则a1>$\frac{1}{c}$-1或a1<1;
(2)证明:对n∈N*用数学归纳法证明an∈(0,1),
当n=1时,a1∈(0,1).假设ak∈(0,1)(k≥1)
则ak+1=cak2+1-c<c+1-c=1,且ak+1=cak2+1-c>1-c>0,
∴ak+1∈(0,1),由数学归纳法知an∈(0,1)对所有n∈N*成立;
(3)证明:由于0<c<$\frac{1}{2}$,
当n=1时,a12>1-$\frac{2}{1-2c}$=$\frac{-1-2c}{1-2c}$,结论成立;
当n≥2时,an+1=can2+1-c,即有1-an+1=c(1-an)(1+an)<2c(1-an),
即1-an<2c(1-an-1)<…<(2c)n-1,
an>1-(2c)n-1>0
∴an2>(1-(2c)n-1)2=1-2(2c)n-1+(2c)2(n-1)>1-2(2c)n-1
∴a12+a22+…+an2=a22+…+an2>n-1-2[2c+(2c)2+…+(2c)n-1]
=n-1-2•$\frac{2c[1-(2c)^{n-1}]}{1-2c}$
=n-1-2•$\frac{2c-(2c)^{n}}{1-2c}$=n+1-2•$\frac{1-(2c)^{n}}{1-2c}$>n+1-$\frac{2}{1-2c}$>n-$\frac{2}{1-2c}$.
故Sn>n-$\frac{2}{1-2c}$成立.
点评 本题考查数列和不等式的综合应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地选用证明方法.


科目:高中数学 来源: 题型:填空题
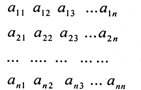 如图表:现有n2(n≥4)个正数排列成n行n列方阵,符号aij(1≤i≤n,1≤j≤n,i,j∈N*)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都相等.若a11=2,a24=a32=16,则aij=2i•j.
如图表:现有n2(n≥4)个正数排列成n行n列方阵,符号aij(1≤i≤n,1≤j≤n,i,j∈N*)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都相等.若a11=2,a24=a32=16,则aij=2i•j.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.65<log0.65<50.6 | B. | 0.65<50.6<log0.65 | ||
| C. | log0.65<0.65<50.6 | D. | log0.65<50.6<0.65 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com