解:(1)由f′(x)=e
x-a,得x=lna,
当a≤0时,f′(x)>0,f(x)的单调递增区间为(-∞,+∞).
当a>0时,f′(x)=e
x-a=0,得x=lna,
x∈(-∞,lna)时,f′(x)<0;x∈(lna,+∞)时,f′(x)>0;
∴f(x)的单减区间为(-∞,lna),单增区间为(lna,+∞),
所以a≤0时,f(x)只有单调递增区间为(-∞,+∞).
a>0时,f(x)的增区间为(lna,+∞),减区间为(-∞,lna).…(5分)
(2)由(1)得f(x)的最小值为f(lna)=a-alna-1,
f(x)≥0对任意的x∈R恒成立,即f(x)
min≥0.
设g(a)=a-alna-1,所以g(a)≥0.
由g′(a)=1-lna-1=-lna=0,得a=1.
∴g(a)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减,
∴g(a)在a=1处取得最大值,而g(1)=0.
因此g(a)≥0的解为a=1,∴a=1.(9分)
(3)证明:由(2)知,对任意实数x均有e
x-x-1≥0,即1+x≤e
x.
令x=-

(n∈N
*,k=0,1,2,3,…,n-1),则0<1-

≤e-

.
∴(1-

)n≤(e-

)n=e-k.
∴(

)
n+(

)
n+…+(

)
n+(
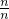
)
n≤e-(n-1)+e-(n-2)+…+e-2+e-1+1
=
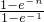
<

=
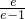
.…(14分)
分析:(1)求导函数,确定函数的单调性,从而可得f(x)在x=lna处取得极小值,且为最小值;
(2)f(x)≥0对任意的x∈R恒成立,即在x∈R上,f(x)
min≥0.由(1),构造函数g(a)=a-alna-1,所以g(a)≥0,确定函数的单调性,即可求得实数a的值;
(3)由(2)知,对任意实数x均有e
x-x-1≥0,即1+x≤e
x,令x=-

(n∈N
*,k=0,1,2,3,…,n-1),可得0<1-

≤e-

,从而有(1-

)n≤(e-

)n=e-k,由此即可证得结论.
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查恒成立问题,同时考查不等式的证明,解题的关键是正确求导数,确定函数的单调性.

 )n+(
)n+( )n+…+(
)n+…+( )n+(
)n+(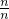 )n<
)n<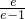 .
. (n∈N*,k=0,1,2,3,…,n-1),则0<1-
(n∈N*,k=0,1,2,3,…,n-1),则0<1- ≤e-
≤e- .
. )n≤(e-
)n≤(e- )n=e-k.
)n=e-k. )n+(
)n+( )n+…+(
)n+…+( )n+(
)n+(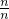 )n≤e-(n-1)+e-(n-2)+…+e-2+e-1+1
)n≤e-(n-1)+e-(n-2)+…+e-2+e-1+1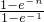 <
< =
=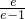 .…(14分)
.…(14分) (n∈N*,k=0,1,2,3,…,n-1),可得0<1-
(n∈N*,k=0,1,2,3,…,n-1),可得0<1- ≤e-
≤e- ,从而有(1-
,从而有(1- )n≤(e-
)n≤(e- )n=e-k,由此即可证得结论.
)n=e-k,由此即可证得结论.

 备战中考寒假系列答案
备战中考寒假系列答案