
分析 (1)利用递推关系即可得出.
(2)利用对数的运算性质、等差数列的通项公式与单调性即可得出.
解答 解:(1)令n=1,得$λa_1^2=2{S_1}=2{a_1},{a_1}(λ{a_1}-2)=0$,因为a1≠0,所以${a_1}=\frac{2}{λ}$,当n≥2时,$2{a_n}=\frac{2}{λ}+{S_n}$,$2{a_{n-1}}=\frac{2}{λ}+{S_{n-1}}$,两式相减得2an-2an-1=an(n≥2),
所以an=2an-1(n≥2),从而数列{an}为等比数列,
所以${a_n}={a_1}•{2^{n-1}}=\frac{2^n}{λ}$.
(2)当a1>0,λ=100时,由(1)知,an=$\frac{{2}^{n}}{100}$,
bn=lg$\frac{1}{{a}_{n}}$=$lg\frac{100}{{2}^{n}}$=2-nlg2.
所以数列{bn}是单调递减的等差数列,公差为-lg2,所以${b_1}>{b_2}>…>{b_6}=lg\frac{100}{2^6}=lg\frac{100}{64}>lg1=0$,
当n≥7时,${b_n}≤{b_7}=lg\frac{100}{2^7}<lg1=0$,所以数列$\{lg\frac{1}{a_n}\}$的前6项和最大.
点评 本题考查了等差数列的通项公式、数列递推关系、数列的单调性、对数的运算性质,考查了推理能力与计算能力,属于中档题.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{a}{a+b}$与$\frac{c}{c+d}$ | B. | $\frac{a}{c+d}$与$\frac{c}{a+b}$ | C. | $\frac{a}{a+b}$与$\frac{c}{b+c}$ | D. | $\frac{a}{b+d}$与$\frac{c}{a+c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -12 | B. | -10 | C. | -4 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1<a<1 | B. | 0<a<1 | C. | a<-1或a>1 | D. | a=±1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 空气质量指数(μg/m3) | 0-50 | 51-100 | 101-150 | 151-200 | 201-250 |
| 空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | m | 10 | 5 |
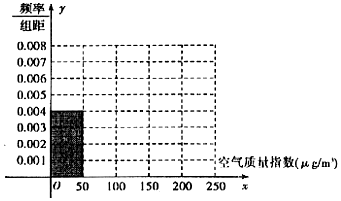
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com