
(本小题满分12分)某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名.现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
分数段 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
男 | 3 | 9 | 18 | 15 | 6 | 9 |
女 | 6 | 4 | 5 | 10 | 13 | 2 |
估计男、女生各自的成绩平均分(同一组数据用该组区间中点值作代表),从计算结果看,判断数学成绩与性别是否有关;
优分 | 非优分 | 合计 | |
男生 | |||
女生 | |||
合计 | 100 |
(2)规定80分以上为优分(含80分),请你根据已知条件作出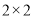 列联表,并判断是否有
列联表,并判断是否有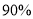 以上的把握认为“数学成绩与性别有关”.
以上的把握认为“数学成绩与性别有关”.
附表及公式
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
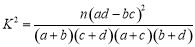 .
.
(1)不能判断;(2)没有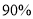 的把握认为“数学成绩与性别有关.
的把握认为“数学成绩与性别有关.
【解析】
试题分析:(1)利用同一组数据用该组区间中点值作代表,计算男女生各自的成绩平均数,即可得出结论;(2)根据所给的条件写出列联表,根据列联表做出观测值,把观测值同临界值进行比较,得到结论.
试题解析:(1)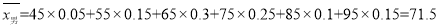 , 2分
, 2分
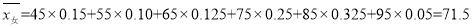 , 4分
, 4分
从男、女生各自的成绩平均分来看,并不能判断数学成绩与性别有关; 5分
(2)由频数分布表可知:在抽取的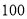 学生中,“男生组”中的优分有
学生中,“男生组”中的优分有 (人),“女生组”中的优分有
(人),“女生组”中的优分有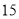 (人),据此可得
(人),据此可得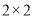 列联表如下:
列联表如下:
优分 | 非优分 | 合计 | |
男生 | 15 | 45 | 60 |
女生 | 15 | 25 | 40 |
合计 | 30 | 70 | 100 |
可得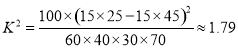 , 10分
, 10分
∵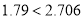 ,∴没有
,∴没有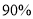 的把握认为“数学成绩与性别有关”. 12分
的把握认为“数学成绩与性别有关”. 12分
考点:独立性检验的运用.


科目:高中数学 来源:2014-2015学年湖北省黄冈市高三上学期元月调研考试文科数学试卷(解析版) 题型:选择题
下列各选项中,正确的是( )
A.若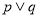 为真命题,则
为真命题,则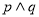 为真命题
为真命题
B.命题“若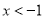 ,则
,则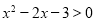 ”的否命题为“若
”的否命题为“若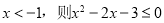 ”
”
C.已知命题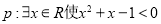 ,则
,则 为:
为: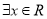 使得
使得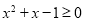
D.设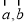 是任意两个向量,则“
是任意两个向量,则“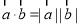 ”是“
”是“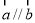 ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省黄冈市高三上学期元月调研考试理科数学试卷(解析版) 题型:选择题
已知O是坐标原点,点 ,若点
,若点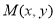 为平面区域
为平面区域 上的一个动点,则
上的一个动点,则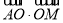 的取值范围是 ( )
的取值范围是 ( )
A.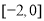 B.
B.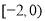 C.
C.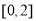 D.
D.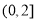
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省九江市第一次高考模拟统一考试文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4—4:坐标系与参数方程
已知直线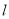 的参数方程为
的参数方程为 (
(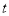 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,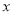 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程是
的极坐标方程是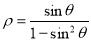 .
.
(1)写出直线 的极坐标方程与曲线
的极坐标方程与曲线 的普通方程;
的普通方程;
(2)若点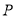 是曲线
是曲线 上的动点,求
上的动点,求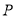 到直线
到直线 距离的最小值,并求出此时
距离的最小值,并求出此时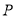 点的坐标.
点的坐标.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省景德镇高三第二质检理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知椭圆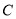 :
: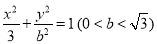 ,其通径(过焦点且与x轴垂直的直线被椭圆截得的线段)长
,其通径(过焦点且与x轴垂直的直线被椭圆截得的线段)长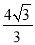 .
.
(1)求椭圆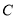 的方程;
的方程;
(2)设过椭圆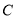 右焦点的直线(不与
右焦点的直线(不与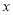 轴重合)与椭圆交于
轴重合)与椭圆交于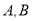 两点,问在
两点,问在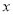 轴上是否存在一点
轴上是否存在一点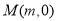 ,使
,使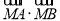 为常数?若存在,求点
为常数?若存在,求点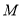 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com