
分析 先求得二项式展开式的通项公式,再令x的幂指数等于3,求得r、r′的值,从而求得x3项的系数.
解答 解:式子(x2+2x-1)5 =[(x2+2x)-1]5展开式的通项公式为:
Tr+1=${C}_{5}^{r}$•(x2+2x)5-r•(-1)r,
对于(x2+2x)5-r,它的通项公式为:
Tr′+1=2r′•${C}_{5-r}^{r′}$•x10-2r-r′,
其中0≤r′≤5-r,0≤r≤5,r、r′都是自然数;
令10-2r-r′=3,可得$\left\{\begin{array}{l}{r=2}\\{r′=3}\end{array}\right.$,或$\left\{\begin{array}{l}{r=3}\\{r′=1}\end{array}\right.$,
所以x3项的系数为:
${C}_{5}^{2}$•23•${C}_{3}^{3}$-${C}_{5}^{3}$•2•${C}_{2}^{1}$=40.
故答案为:40.
点评 本题主要考查了二项式定理以及二项式展开式的通项公式应用问题,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
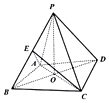 如图,在四棱锥P-ABCD中,∠BAD=120°,AB=AD=2,△BCD是等边三角形,E是BP中点,AC与BD交于点O,且OP⊥平面ABCD.
如图,在四棱锥P-ABCD中,∠BAD=120°,AB=AD=2,△BCD是等边三角形,E是BP中点,AC与BD交于点O,且OP⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{5}}{2}$-1 | B. | $\frac{3\sqrt{3}}{2}$-1 | C. | 2$\sqrt{3}$-1 | D. | $\sqrt{10}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com