
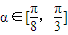 时,点A的纵坐标y的取值范围是 .
时,点A的纵坐标y的取值范围是 .  ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
| π |
| 8 |
| π |
| 3 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011届浙江省杭州市萧山九中高三寒假作业数学卷一 题型:单选题
如右图,在平面直角坐标系xoy 中,A(1,0),B(1,1),
|
查看答案和解析>>
科目:高中数学 来源:2011年湖南省高三第一次学情摸底考试数学卷 题型:选择题
如右图,在平面直角坐标系xoy 中,A(1,0),B(1,1),
C(0,1),映射f 将xOy 平面上的点P(x,y)对应到另一
个平面直角坐标系uo′v 上的点P′(2xy,x2 – y2),则当点
|
轨迹是 ( )
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市高三寒假作业数学卷一 题型:选择题
如右图,在平面直角坐标系xoy 中,A(1,0),B(1,1),
|
个平面直角坐标系uo′v 上的点P′(2xy,x2 – y2),则当点
P 沿着折线A—B—C 运动时,在映射f 的作用下,动点P′的
轨迹是( )
查看答案和解析>>
科目:高中数学 来源:2013届浙江省高二第一学期期末考试文科数学 题型:解答题
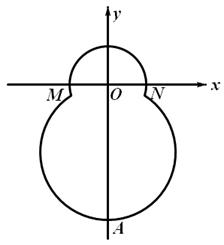
如右图,在平面直角坐标系 中,已知“葫芦”曲线
中,已知“葫芦”曲线 由圆弧
由圆弧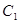 与圆弧
与圆弧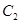 相接而成,两相接点
相接而成,两相接点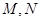 均在直线
均在直线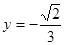 上.圆弧
上.圆弧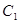 所在圆的圆心是坐标原点
所在圆的圆心是坐标原点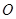 ,半径为
,半径为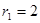 ;圆弧
;圆弧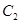 过点
过点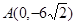 .
.
(I)求圆弧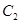 的方程;
的方程;
(II)已知直线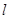 :
: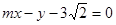 与“葫芦”曲线
与“葫芦”曲线 交于
交于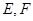 两点.当
两点.当 时,求直线
时,求直线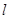 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com