
【题目】若函数![]() 在区间
在区间![]() 上存在零点,则实数
上存在零点,则实数![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】在水平地面上的不同两点处栽有两根笔直的电线杆,假设它们都垂直于地面,则在水平地面上视它们上端仰角相等的点![]() 的轨迹可能是( )
的轨迹可能是( )
①直线 ②圆 ③椭圆 ④抛物线
A.①②B.①③C.①②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,以
为极点,以![]() 轴为非负半轴为极轴建立极坐标系,两坐标系相同的长度单位.圆
轴为非负半轴为极轴建立极坐标系,两坐标系相同的长度单位.圆![]() 的方程为
的方程为![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站举行“卫生防疫”的知识竞赛网上答题,共有120000人通过该网站参加了这次竞赛,为了解竞赛成绩情况,从中抽取了100人的成绩进行统计,其中成绩分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其频率分布直方图如图所示,请你解答下列问题:
,其频率分布直方图如图所示,请你解答下列问题:
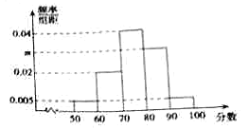
(1)求![]() 的值;
的值;
(2)成绩不低于90分的人就能获得积分奖励,求所有参赛者中获得奖励的人数;
(3)根据频率分布直方图,估计这次知识竞赛成绩的平均分(用组中值代替各组数据的平均值).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知线段![]() 是过抛物线
是过抛物线![]() 的焦点F的一条弦,过点A(A在第一象限内)作直线
的焦点F的一条弦,过点A(A在第一象限内)作直线![]() 垂直于抛物线的准线,垂足为C,直线
垂直于抛物线的准线,垂足为C,直线![]() 与抛物线相切于点A,交x轴于点T,给出下列命题:
与抛物线相切于点A,交x轴于点T,给出下列命题:
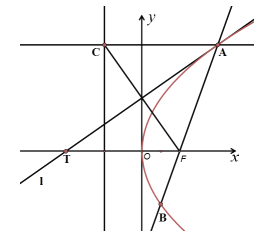
(1)![]() ;
;
(2)![]() ;
;
(3)![]() .
.
其中正确的命题个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人在相同条件下各射击![]() 次,每次中靶环数情况如图所示:
次,每次中靶环数情况如图所示:
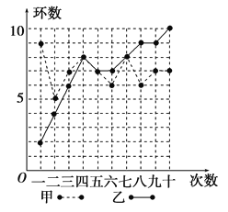
(1)请填写下表(先写出计算过程再填表):
平均数 | 方差 | 命中 | |
甲 |
|
|
|
乙 |
(2)从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中![]() 环及
环及![]() 环以上的次数相结合看(分析谁的成绩好些);
环以上的次数相结合看(分析谁的成绩好些);
③从折线图上两人射击命中环数的走势看(分析谁更有潜力).
参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①已知直线![]() 、
、![]() 和平面
和平面![]() ,若
,若![]() ,
,![]() ,则
,则![]() ;
;
②平面上到一个定点和一条定直线的距离相等的点的轨迹是一条抛物线;
③双曲线![]() ,则直线
,则直线![]()
![]() 与双曲线有且只有一个公共点;
与双曲线有且只有一个公共点;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直;
⑤过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 中点为
中点为![]() ,设直线
,设直线![]() 斜率为
斜率为![]()
![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则
,则![]() 等于
等于![]() .
.
其中,正确命题的序号为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a∈R且a≠0).
(a∈R且a≠0).
(1)当a![]() 时,求曲线y=f(x)在点(1,f(1))处的切线方程;
时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性与单调区间;
(3)若y=f(x)有两个极值点x1,x2,证明:f(x1)+f(x2)<9﹣lna.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com