
分析 利用余弦定理化简已知等式可求b2+c2-a2=bc,进而利用余弦定理可求cosA=$\frac{1}{2}$,可得A=$\frac{π}{3}$,C=$\frac{2π}{3}$-B,利用三角函数恒等变换的应用化简可得$\sqrt{3}$cosC-2sinB=-sin(B+$\frac{π}{3}$),进而利用正弦函数的图象和性质可求最小值.
解答 解:在△ABC中,∵$\frac{cosA}{cosB+cosC}$=$\frac{a}{b+c}$,
∴$\frac{\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}}{\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}+\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}}$=$\frac{a}{b+c}$,整理可得:b2+c2-a2=bc,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{1}{2}$,
∴A=$\frac{π}{3}$,C=$\frac{2π}{3}$-B,
∴$\sqrt{3}$cosC-2sinB=$\sqrt{3}$cos($\frac{2π}{3}$-B)-2sinB=-$\frac{1}{2}$sinB-$\frac{\sqrt{3}}{2}$cosB=-sin(B+$\frac{π}{3}$)≥-1,当B+$\frac{π}{3}$=$\frac{π}{2}$时等号成立,
即当B=$\frac{π}{6}$,C=$\frac{π}{2}$时,$\sqrt{3}$cosC-2sinB的最小值为-1.
故答案为:-1.
点评 本题主要考查了三角函数恒等变换的应用,余弦定理在解三角形中的综合应用,考查了学生的运算求解能力和转化思想,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\overrightarrow{BC}$ | C. | $\overrightarrow{DA}$ | D. | $\overrightarrow 0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
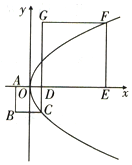 如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )
如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $1-\frac{{\sqrt{2}}}{2}$ | C. | $2+\sqrt{2}$ | D. | $2-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{1}{4},+∞)$ | B. | $(-\frac{1}{2},0)$ | C. | (-1,0) | D. | $(-\frac{1}{4},0)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com