
【题目】已知函数![]() ,
,![]() .
.
(1)求![]() 的极值;
的极值;
(2)若方程![]() 有三个解,求实数
有三个解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,极小值
时,极小值![]() ;当
;当![]() 时,无极值;当
时,无极值;当![]() 时,极大值
时,极大值![]() ;(2)
;(2)![]()
【解析】
(1)求得![]() 的定义域和导函数,对
的定义域和导函数,对![]() 分成
分成![]() 三种情况进行分类讨论
三种情况进行分类讨论 ![]() 的极值.
的极值.
(2)构造函数![]() ,通过
,通过![]() 的导函数
的导函数![]() 研究
研究![]() 的零点,对
的零点,对![]() 分成
分成![]() 进行分类讨论,结合
进行分类讨论,结合![]() 有三个零点,求得
有三个零点,求得![]() 的取值范围.
的取值范围.
(1)![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,所以
上递增,所以![]() 在
在![]() 处取得极小值
处取得极小值![]() ,
,
当![]() 时,
时,![]() ,所以无极值,
,所以无极值,
当![]() 时,
时,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,所以
上递减,所以![]() 在
在![]() 处取得极大值
处取得极大值![]() .
.
(2)设![]() ,即
,即![]() ,
,
![]()
![]()
![]() .
.
①若![]() ,则当
,则当![]() 时,
时,![]() ,
,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,![]() 至多有两个零点.
至多有两个零点.
②若![]() ,则
,则![]() ,
,![]() (仅
(仅![]() ).
).![]() 单调递增,
单调递增,![]() 至多有一个零点.
至多有一个零点.
③若![]() ,则
,则![]() ,当
,当![]() 或
或![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减,要使
单调递减,要使![]() 有三个零点,必须有
有三个零点,必须有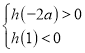 成立.
成立.
由![]() ,得
,得![]() ,这与
,这与![]() 矛盾,所以
矛盾,所以![]() 不可能有三个零点.
不可能有三个零点.
④若![]() ,则
,则![]() .当
.当![]() 或
或![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减,要使
单调递减,要使![]() 有三个零点,必须有
有三个零点,必须有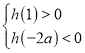 成立,
成立,
由![]() ,得
,得![]() ,由
,由![]() 及
及![]() ,得
,得![]() ,
,
![]() .
.
并且,当![]() 时,
时,![]() ,
,![]() ,
,![]()
![]() ,
,![]() .
.
综上,使![]() 有三个零点的
有三个零点的![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】定义:如果数列![]() 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称![]() 为“三角形”数列,对于“三角形”数列
为“三角形”数列,对于“三角形”数列![]() ,如果函数
,如果函数![]() 使得
使得![]() 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称![]() 是数列
是数列![]() 的“保三角形函数”,
的“保三角形函数”,![]() .
.
(1)已知![]() 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若![]() 是数列
是数列![]() 的“保三角形函数”,求
的“保三角形函数”,求![]() 的取值范围;
的取值范围;
(2)已知数列![]() 的首项为2010,
的首项为2010,![]() 是数列
是数列![]() 的前
的前![]() 项和,且满足
项和,且满足![]() ,证明
,证明![]() 是“三角形”数列;
是“三角形”数列;
(3)根据“保三角形函数的定义,对函数![]() ,和数列1,
,和数列1,![]() 提出一个正确的命题,并说明理由.
提出一个正确的命题,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面![]() 上的一列点
上的一列点![]() ,简记为
,简记为![]() .若由
.若由![]() 构成的数列
构成的数列![]() 满足
满足![]() ,其中
,其中![]() 为方向与
为方向与![]() 轴正方向相同的单位向量,则称
轴正方向相同的单位向量,则称![]() 为
为![]() 点列.
点列.
(1)判断![]() ,是否为
,是否为![]() 点列,并说明理由;
点列,并说明理由;
(2)若![]() 为
为![]() 点列,且点
点列,且点![]() 在点
在点![]() 的右上方.任取其中连续三点
的右上方.任取其中连续三点![]() ,判断
,判断![]() 的形状(锐角三角形、直角三角形、钝角三角形),并予以证明;
的形状(锐角三角形、直角三角形、钝角三角形),并予以证明;
(3)若![]() 为
为![]() 点列,正整数
点列,正整数![]() ,满足
,满足![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,
, ![]() 为
为![]() 上一点,
上一点,![]() 为菱形
为菱形![]() 对角线的交点.
对角线的交点.
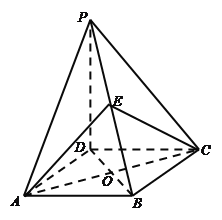
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,四棱锥
,四棱锥![]() 的体积是四棱锥
的体积是四棱锥![]() 的体积的
的体积的![]() ,求二面角
,求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点F的距离为
到焦点F的距离为![]() .
.
(1)求抛物线M的方程;
(2)过点F斜率为k的直线l与M相交于C,D两点,线段![]() 的垂直平分线
的垂直平分线![]() 与M相交于
与M相交于![]() 两点,点
两点,点![]() 分别为线段
分别为线段![]() 和
和![]() 的中点.
的中点.
①试用k表示点![]() 的坐标;
的坐标;
②若以线段![]() 为直径的圆过点C,求直线l的方程.
为直径的圆过点C,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥P﹣ABCD的底面边长为2,侧棱长为2![]() ,过点A作一个与侧棱PC垂直的平面α,则平面α被此正四棱锥所截的截面面积为_____,平面α将此正四棱锥分成的两部分体积的比值为_____.
,过点A作一个与侧棱PC垂直的平面α,则平面α被此正四棱锥所截的截面面积为_____,平面α将此正四棱锥分成的两部分体积的比值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年2月份,我国武汉地区爆发了新冠肺炎疫情,为了预防疫情蔓延,全国各大医药厂商纷纷加紧生产口罩,某医疗器械生产工厂为了解目前的生产力,统计了每个工人每小时生产的口罩数量(单位:箱),得到如图所示的频率分布直方图,其中每个工人每小时的产量均落在[10,70]内,数据分组为[10,20)、[20,30)、[30,40)、[40,50)、[50,60)、![]() ,已知前三组的频率成等差数列,第三组、第四组、第五组的频率成等比数列,最后一组的频率为
,已知前三组的频率成等差数列,第三组、第四组、第五组的频率成等比数列,最后一组的频率为![]() .
.
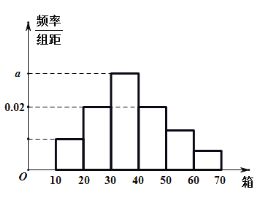
(1)求实数a的值;
(2)在最后三组中采用分层抽样的方法随机抽取了6人,现从这6人中随机抽出两人对其它小组的工人进行生产指导,求这两人来自同一小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商家通常依据“乐观系数准则”确定商品销售价格,及根据商品的最低销售限价a,最高销售限价b(b>a)以及常数x(0<x<1)确定实际销售价格c=a+x(b﹣a),这里,x被称为乐观系数.
经验表明,最佳乐观系数x恰好使得(c﹣a)是(b﹣c)和(b﹣a)的等比中项,据此可得,最佳乐观系数x的值等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com