
已知函数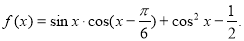
(1)求函数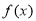 的最大值,并写出
的最大值,并写出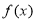 取最大值
取最大值 时的取值集合;
时的取值集合;
(2)在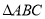 中,角
中,角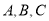 的对边分别为
的对边分别为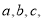 ,若
,若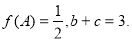 求
求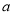 的最小值.
的最小值.
 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源:2013-2014学年河南省毕业班高考适应性模拟练习理科数学试卷(解析版) 题型:填空题
已知P为三角形ABC内部任一点(不包括边界),且满足 ,则?ABC的形状一定为___________.
,则?ABC的形状一定为___________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省原名校高三高考仿真模拟统一考试文科数学试卷(解析版) 题型:解答题
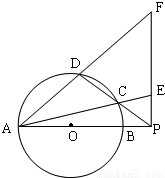
如图,圆O的直径AB= 10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C、D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
(Ⅰ)求证: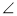 PEC=
PEC= 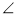 PDF
PDF
(Ⅱ)求PE PF的值
PF的值
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省原名校高三高考仿真模拟统一考试文科数学试卷(解析版) 题型:选择题
已知正方形ABCD,其中顶点A、C坐标分别是 (2,0)、(2,4),点P(x,y)在正方形内部(包括边界)上运动,则 的最大值是
的最大值是
A.10 B.8 C.12 D.6
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南中原名校高三下学期第二次联考理科数学试卷(解析版) 题型:解答题
如图,在锐角三角形ABC中,D 为C在AB上的射影,E 为D在BC上的射影,F为DE上一点,且满足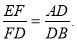
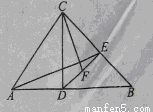
(1)证明: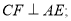 (2)若AD=2,CD=3.DB=4,求
(2)若AD=2,CD=3.DB=4,求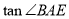 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南中原名校高三下学期第二次联考理科数学试卷(解析版) 题型:选择题
将数字1,2,3,4填入右侧表格内,要求每行、每列的数字互不相同,如图所示,则不同的填表方式共有( )种.
1 | 2 | 3 | 4 |
4 | 3 | 1 | 2 |
2 | 1 | 4 | 3 |
3 | 4 | 2 | 1 |
A.432 B.576 C.720 D.864
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南中原名校高三下学期第二次联考理科数学试卷(解析版) 题型:选择题
一个空间几何体的三视图如图,则该几何体的体积为( )
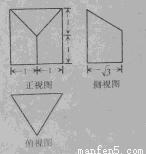
A. 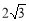 B.
B. 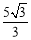 C.
C. 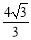 D.
D. 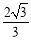
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省邯郸市高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
如图,在斜三棱柱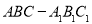 中,侧面
中,侧面 ⊥底面
⊥底面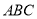 ,侧棱
,侧棱 与底面
与底面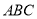 成60°的角,
成60°的角, .底面
.底面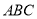 是边长为2的正三角形,其重心为
是边长为2的正三角形,其重心为 点,
点, 是线段
是线段 上一点,且
上一点,且 .
.
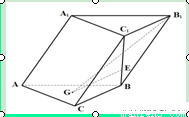
(1)求证: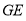 //侧面
//侧面 ;
;
(2)求平面 与底面
与底面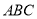 所成锐二面角的余弦值;
所成锐二面角的余弦值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com