
 小题满分10分)
小题满分10分) 盖长方体水池
盖长方体水池 ,底面一边长固定为8
,底面一边长固定为8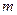 ,
, 最大装水量为72
最大装水量为72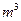 ,池底和池壁的造价分别为
,池底和池壁的造价分别为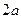 元
元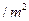 、
、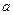 元
元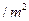 ,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
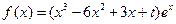 ,
,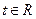 .
.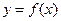 依次在
依次在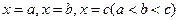 处取到极值.
处取到极值.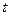 的取值范围;
的取值范围;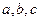 成等差数列,求
成等差数列,求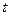 的值
的值 .
.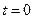 时
时 ,对任意的
,对任意的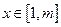 ,不等式
,不等式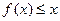 恒成立.求正整数
恒成立.求正整数 的最大值.
的最大值. 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.sin x | B.-sin x |
| C.cos x | D.-cos x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
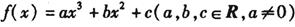 的图象过点P( 1,2),且在点P处的切线与直线x-3y=0垂直.
的图象过点P( 1,2),且在点P处的切线与直线x-3y=0垂直.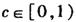 ,试求函数f(x)的单调区间;
,试求函数f(x)的单调区间;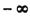 ,m),(n,
,m),(n,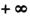 )是f(x)的单调递增区间,试求n-m-2c的范围
)是f(x)的单调递增区间,试求n-m-2c的范围查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com