
【题目】市政府为了促进低碳环保的出行方式,从全市在册的50000辆电动车中随机抽取100辆,委托专业机构免费为它们进行电池性能检测.电池性能分为需要更换、尚能使用、较好、良好四个等级,并分成电动自行车和电动汽车两个群体分别进行统计,样本分布如下图.
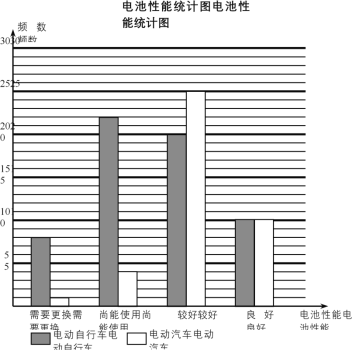
(1)从电池性能较好的电动车中,采用分层抽样的方法随机抽取了9辆,求再从这9辆电动车中随机抽取2辆,至少有1辆为电动汽车的概率;
(2)为提高市民对电动车的使用热情,市政府准备为电动车车主一次性发放补助,标准如下:
①电动自行车每辆补助300元;
②电动汽车每辆补助500元;
③对电池需要更换的电动车每辆额外补助400元.
利用样本估计总体,试估计市政府执行此方案的预算(单位:万元).
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】若一条直线与一个平面垂直,则称此直线与平面构成一个“正交线面对”.那么在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( )
A. 48 B. 36 C. 24 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问110名性别不同的大学生是否爱好体育,得到表:

参照附表,得到的正确结论是![]()
![]()
附:由公式算得:![]()
附表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 1.323 | 2.702 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
A. 有![]() 以上的把握认为“爱好体育运动与性别有关”
以上的把握认为“爱好体育运动与性别有关”
B. 有![]() 以上的把握认为“爱好体育运动与性别无关”
以上的把握认为“爱好体育运动与性别无关”
C. 在犯错误的概率不超过![]() 的前提下,认为“爱好体育运动与性别有关”
的前提下,认为“爱好体育运动与性别有关”
D. 在犯错误的概率不超过![]() 的前提下,认为“爱好体育运动与性别无关”
的前提下,认为“爱好体育运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体![]() 中,写出所有
中,写出所有
(1)与直线AB平行的直线,并用“∥”表示;
(2)与直线![]() 异面的直线;
异面的直线;
(3)与直线AB平行的平面,并用合适的符号表示;
(4)与平面![]() 平行的平面,并用合适的符号表示;
平行的平面,并用合适的符号表示;
(5)与直线AD垂直的平面,并用合适的符号表示.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图1)的平面展开图(如图2)中,四边形
(如图1)的平面展开图(如图2)中,四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:
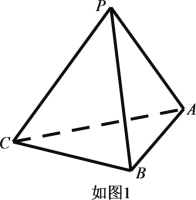

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若点![]() 在棱
在棱![]() 上运动,当直线
上运动,当直线![]() 与平面
与平面![]() 所成的角最大时,求二面角
所成的角最大时,求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.

(1)证明:MN∥平面C1DE;
(2)求AM与平面A1MD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学在高二下学期开设四门数学选修课,分别为《数学史选讲》.《球面上的几何》.《对称与群》.《矩阵与变换》.现有甲.乙.丙.丁四位同学从这四门选修课程中选修一门,且这四位同学选修的课程互不相同,下面关于他们选课的一些信息:①甲同学和丙同学均不选《球面上的几何》,也不选《对称与群》:②乙同学不选《对称与群》,也不选《数学史选讲》:③如果甲同学不选《数学史选讲》,那么丁同学就不选《对称与群》.若这些信息都是正确的,则丙同学选修的课程是( )
A. 《数学史选讲》B. 《球面上的几何》C. 《对称与群》D. 《矩阵与变换》
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com