
分析 (1)由${a_1}=\frac{5}{4}$,且an+1=$\left\{\begin{array}{l}{\frac{1}{2}{a}_{n},n为偶数}\\{{a}_{n}+\frac{1}{4},n为奇数}\end{array}\right.$,记${b_n}={a_{2n-1}}-\frac{1}{4}$,可得b1=a1-$\frac{1}{4}$,a2=${a}_{1}+\frac{1}{4}$,b2=a3-$\frac{1}{4}$=$\frac{1}{2}{a}_{2}$-$\frac{1}{4}$.
(2)b1=1≠0,利用$\frac{{{b_{n+1}}}}{b_n}=\frac{{{a_{2n+1}}-\frac{1}{4}}}{{{a_{2n-1}}-\frac{1}{4}}}=\frac{{\frac{1}{2}{a_{2n}}-\frac{1}{4}}}{{{a_{2n-1}}-\frac{1}{4}}}=\frac{{\frac{1}{2}({a_{2n-1}}+\frac{1}{4})-\frac{1}{4}}}{{{a_{2n-1}}-\frac{1}{4}}}=\frac{{\frac{1}{2}{a_{2n-1}}-\frac{1}{8}}}{{{a_{2n-1}}-\frac{1}{4}}}=\frac{1}{2}$,即可证明.
(3)${c_n}=({b_n}+\frac{1}{4})•({b_n}-1)={({b_n}-\frac{3}{8})^2}-\frac{25}{64}$,bn∈(0,1],设bn=t∈(0,1],$y={({t-\frac{3}{8}})^2}-\frac{25}{64}$,当n=2时,当n=3时,即可得出.
解答 解:(1)由${a_1}=\frac{5}{4}$,且an+1=$\left\{\begin{array}{l}{\frac{1}{2}{a}_{n},n为偶数}\\{{a}_{n}+\frac{1}{4},n为奇数}\end{array}\right.$,记${b_n}={a_{2n-1}}-\frac{1}{4}$,
∴b1=a1-$\frac{1}{4}$=1,a2=${a}_{1}+\frac{1}{4}$=$\frac{3}{2}$,b2=a3-$\frac{1}{4}$=$\frac{1}{2}{a}_{2}$-$\frac{1}{4}$=$\frac{1}{2}×\frac{3}{2}-\frac{1}{4}$=$\frac{1}{2}$.(2分)
(2)b1=1≠0,
$\frac{{{b_{n+1}}}}{b_n}=\frac{{{a_{2n+1}}-\frac{1}{4}}}{{{a_{2n-1}}-\frac{1}{4}}}=\frac{{\frac{1}{2}{a_{2n}}-\frac{1}{4}}}{{{a_{2n-1}}-\frac{1}{4}}}=\frac{{\frac{1}{2}({a_{2n-1}}+\frac{1}{4})-\frac{1}{4}}}{{{a_{2n-1}}-\frac{1}{4}}}=\frac{{\frac{1}{2}{a_{2n-1}}-\frac{1}{8}}}{{{a_{2n-1}}-\frac{1}{4}}}=\frac{1}{2}$,
∴{bn}是以1为首项,$\frac{1}{2}$为公比的等比数列. …(6分)
(3)${c_n}=({b_n}+\frac{1}{4})•({b_n}-1)={({b_n}-\frac{3}{8})^2}-\frac{25}{64}$,bn∈(0,1],…(8分)
设bn=t∈(0,1],$y={({t-\frac{3}{8}})^2}-\frac{25}{64}$,
当n=2时,$t=\frac{1}{2}$,$y=-\frac{3}{8}$;
当n=3时,$t=\frac{1}{4}$,$y=-\frac{3}{8}$;…(10分)
故存在k=2,3使得${c_k}=-\frac{3}{8}$满足题意.…(12分)
点评 本题考查了等比数列的通项公式、递推关系、分类讨论方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
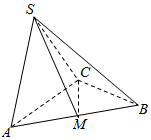 如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC=SA=SC,M为AB的中点.
如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC=SA=SC,M为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 有一个容量为100的样本,其频率分布直方图如图所示,根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为( )
有一个容量为100的样本,其频率分布直方图如图所示,根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为( )| A. | 18 | B. | 36 | C. | 54 | D. | 72 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{5π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 31 | B. | 161 | C. | 30 | D. | 32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com