
已知点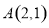 在抛物线
在抛物线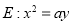 上,直线
上,直线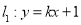 (
(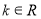 ,且
,且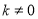 )与抛物线
)与抛物线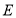 ,相交于
,相交于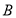 、
、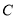 两点,直线
两点,直线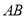 、
、 分别交直线
分别交直线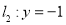 于点
于点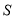 、
、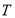 .
.
(1)求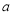 的值;
的值;
(2)若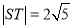 ,求直线
,求直线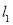 的方程;
的方程;
(3)试判断以线段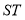 为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
(1)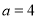 ;(2)
;(2)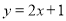 或
或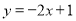 ;(3)存在,且两个定点坐标为
;(3)存在,且两个定点坐标为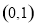 和
和 .
.
【解析】
试题分析:(1)将点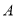 代入抛物线的方程即可求出
代入抛物线的方程即可求出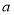 的值;(2)解法1是先设点
的值;(2)解法1是先设点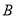 、
、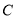 的坐标分别为
的坐标分别为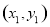 、
、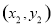 ,将直线
,将直线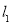 的方程与抛物线
的方程与抛物线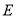 的方程联立求出
的方程联立求出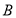 、
、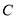 的坐标,并求出
的坐标,并求出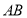 、
、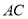 的直线方程,与直线
的直线方程,与直线 的方程联立求出
的方程联立求出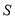 、
、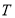 的坐标,利用两点间的距离公式列等式求出
的坐标,利用两点间的距离公式列等式求出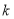 的值,从而求出直线
的值,从而求出直线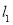 的方程;解法2是设直线
的方程;解法2是设直线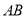 的方程为
的方程为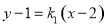 ,点
,点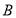 的坐标为
的坐标为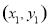 ,分别将直线
,分别将直线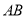 的方程与抛物线和直线
的方程与抛物线和直线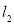 的方程求出点
的方程求出点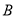 、
、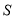 的坐标,然后设直线
的坐标,然后设直线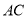 的方程为
的方程为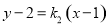 ,利用同样的方法求出点
,利用同样的方法求出点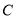 、
、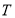 的坐标,利用点
的坐标,利用点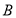 、
、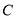 都在直线
都在直线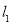 上,结合两点连线的斜率等于
上,结合两点连线的斜率等于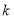 值以及点
值以及点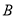 在直线
在直线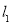 得到
得到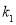 、
、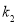 与
与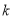 之间的等量关系,然后再利用两点间的距离公式列等式求出
之间的等量关系,然后再利用两点间的距离公式列等式求出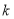 的值,从而求出直线
的值,从而求出直线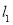 的方程;(3)解法1是求出线段
的方程;(3)解法1是求出线段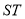 的中点的坐标,然后写出以
的中点的坐标,然后写出以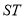 为直径的圆的方程,结合韦达定理进行化简,根据方程的结构特点求出定点的坐标;解法2是设
为直径的圆的方程,结合韦达定理进行化简,根据方程的结构特点求出定点的坐标;解法2是设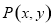 为以
为以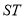 为直径的圆上的一点,由
为直径的圆上的一点,由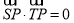 得到以
得到以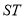 为直径的圆的方程,然后圆的方程的结构特点求出定点的坐标.
为直径的圆的方程,然后圆的方程的结构特点求出定点的坐标.
试题解析:(1)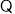 点
点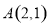 在抛物线
在抛物线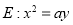 上,
上,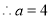 .
.
第(2)、(3)问提供以下两种解法:
解法1:(2)由(1)得抛物线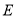 的方程为
的方程为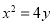 .
.
设点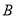 、
、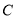 的坐标分别为
的坐标分别为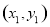 、
、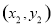 ,依题意,
,依题意,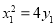 ,
,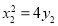 ,
,
由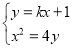 消去
消去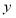 得
得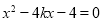 ,
,
解得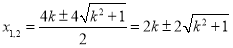 .
.
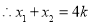 ,
,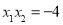 ,
,
直线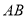 的斜率
的斜率 ,
,
故直线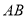 的方程为
的方程为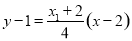 .
.
令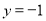 ,得
,得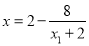 ,
, 点
点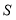 的坐标为
的坐标为 .
.
同理可得点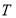 的坐标为
的坐标为 .
.
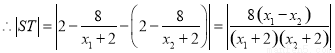
 .
.
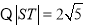 ,
,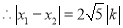 .
.
由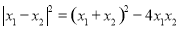 ,得
,得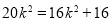 ,
,
解得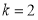 ,或
,或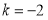 ,
,
 直线
直线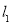 的方程为
的方程为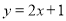 ,或
,或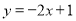 .
.
(3)设线段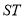 的中点坐标为
的中点坐标为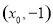 ,
,
则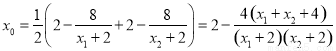
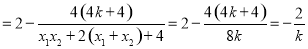 .
.
而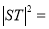
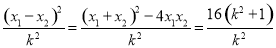 ,
,
 以线段
以线段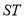 为直径的圆的方程为
为直径的圆的方程为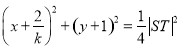
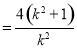 .
.
展开得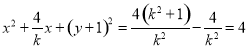 .
.
令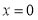 ,得
,得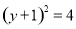 ,解得
,解得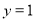 或
或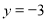 .
.
 以线段
以线段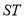 为直径的圆恒过两个定点
为直径的圆恒过两个定点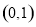 、
、 .
.
解法2:(2)由(1)得抛物线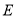 的方程为
的方程为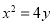 .
.
设直线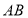 的方程为
的方程为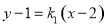 ,点
,点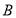 的坐标为
的坐标为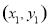 ,
,
由 解得
解得
 点
点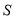 的坐标为
的坐标为 .
.
由 ,消去
,消去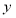 ,得
,得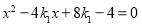 ,
,
即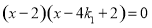 ,解得
,解得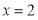 或
或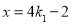 .
.
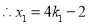 ,
,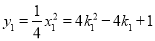 .
.
 点
点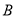 的坐标为
的坐标为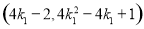 .
.
同理,设直线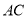 的方程为
的方程为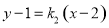 ,
,
则点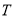 的坐标为
的坐标为 ,点
,点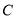 的坐标为
的坐标为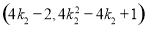 .
.
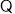 点
点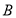 、
、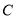 在直线
在直线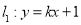 上,
上,
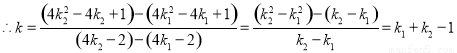 .
.
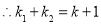 . 5分
. 5分
又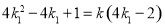
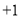 ,得
,得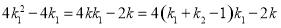 ,
,
化简得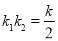 .
.
 ,
,
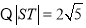 ,
,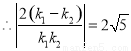 .
.
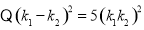 .
.
由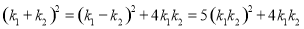 ,
,
得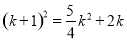 ,
,
解得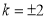 .
.
 直线
直线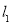 的方程为
的方程为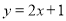 ,或
,或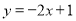 .
.
(3)设点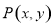 是以线段
是以线段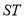 为直径的圆上任意一点,
为直径的圆上任意一点,
则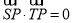 ,
,
得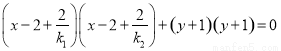 ,
,
整理得,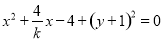 .
.
令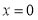 ,得
,得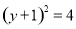 ,解得
,解得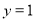 或
或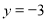 .
.
 以线段
以线段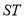 为直径的圆恒过两个定点
为直径的圆恒过两个定点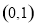 、
、 .
.
考点:1.抛物线的方程;2.直线与抛物线的位置关系;3.两点间的距离;4.韦达定理


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源:2013-2014学年广东省揭阳市高三3月第一次模拟考试理科数学试卷(解析版) 题型:选择题
设点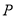 是函数
是函数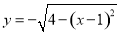 图象上的任意一点,点
图象上的任意一点,点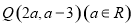 ,则
,则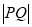 的最小值为( )
的最小值为( )
A.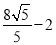 B.
B.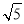 C.
C.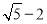 D.
D.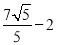
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省惠州市高三4月模拟考试文科数学试卷(解析版) 题型:选择题
设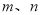 是两条不同的直线,
是两条不同的直线,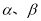 是两个不同的平面。下列四个命题正确的是( )
是两个不同的平面。下列四个命题正确的是( )
A.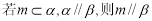 B.
B.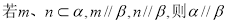
C.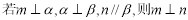 D.
D.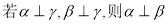
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省广州市毕业班综合测试二理科数学试卷(解析版) 题型:选择题
有两张卡片,一张的正反面分别写着数字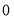 与
与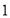 ,另一张的正反面分别写着数字
,另一张的正反面分别写着数字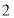 与
与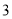 ,将两张卡片排在一起组成一个两位数,则所组成的两位数为奇数的概率是( )
,将两张卡片排在一起组成一个两位数,则所组成的两位数为奇数的概率是( )
A.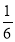 B.
B.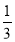 C.
C.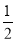 D.
D.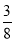
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省广州市毕业班综合测试二文科数学试卷(解析版) 题型:选择题
设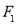 、
、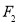 分别是椭圆
分别是椭圆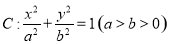 的左、右焦点,点
的左、右焦点,点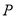 在椭圆
在椭圆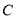 上,线段
上,线段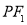 的中点在
的中点在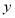 轴上,若
轴上,若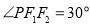 ,则椭圆的离心率为( )
,则椭圆的离心率为( )
A.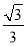 B.
B.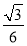 C.
C.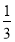 D.
D.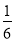
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三第二次模拟考试理科数学试卷(解析版) 题型:填空题
已知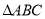 的内角
的内角 、
、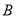 、
、 的对边分别为
的对边分别为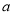 、
、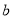 、
、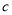 ,且
,且 ,
,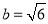 ,
,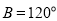 ,则
,则
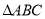 的面积等于________.
的面积等于________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com