
(12分)已知如图:平行四边形ABCD中,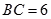 ,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.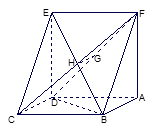
(1)求证:GH∥平面CDE;
(2)若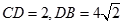 ,求四棱锥F-ABCD的体积.
,求四棱锥F-ABCD的体积.
(1)见解析;(2)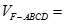
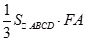 =
=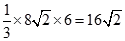 。
。
解析试题分析:(1)证明GH∥平面CDE,利用线面平行的判定定理,只需证明HG∥CD;
(2)证明FA⊥平面ABCD,求出SABCD,即可求得四棱锥F-ABCD的体积.
考点:本试题主要考查了线面平行,考查四棱锥的体积,属于中档题
点评:解决该试题的关键是正确运用线面平行的判定。
解:∵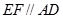 ,
,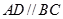 ∴
∴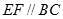 且
且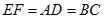
∴四边形EFBC是平行四边形 ∴H为FC的中点--------2分
又∵G是FD的中点
∴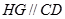 ----------------------------------------4分
----------------------------------------4分
∵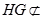 平面CDE,
平面CDE,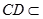 平面CDE
平面CDE
∴GH∥平面CDE --------------------------------------------------6分
(2)∵平面ADEF⊥平面ABCD,交线为AD
且FA⊥AD,
∴FA⊥平面ABCD. --------------------------------------------8
∵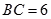 , ∴
, ∴ 又∵
又∵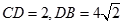 ,
,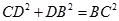
∴BD⊥CD----------------------------------------------------------10分
∴ 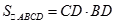 =
=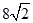
∴ 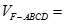
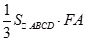 =
=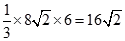 ---------------------12分
---------------------12分


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图示,AB是圆柱的母线,BD是圆柱底面圆的直径,C是底面圆周上一点,E是AC中点,且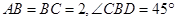 .
.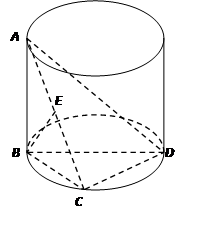
(1)求证: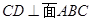 ;
;
(2)求直线BD与面ACD所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题10分)如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出
(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(2)按照给出的尺寸,求该多面体的体积;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,直角梯形ABCD中,∠B=90°,AD//BC,AD=1,BC=2,
∠C=60°,将该梯形绕着AB所在的直线为轴旋转一周,求该旋转体的表面积和体积。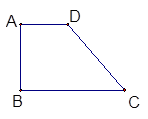
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图4,已知平面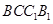 是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线
是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线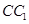 的中点,已知
的中点,已知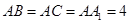
(I))求证: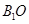 ⊥平面
⊥平面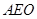 ;
;
(II)求二面角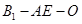 的余弦值.
的余弦值.
(Ⅲ)求三棱锥 的体积.
的体积. 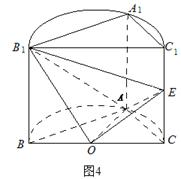
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题8分)如图,ABCD是正方形,O是正方形的中心, PO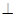 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。
求证:(1)PA∥平面BDE (2)平面PAC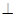 平面BDE
平面BDE
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
用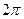 平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为
平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为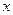 ,圆锥母线的长为
,圆锥母线的长为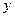
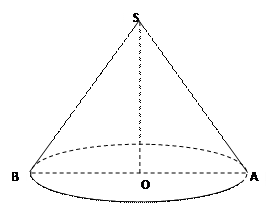
(1)、建立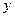 与
与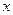 的函数关系式,并写出
的函数关系式,并写出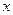 的取值范围;(6分)
的取值范围;(6分)
(2)、圆锥的母线与底面所成的角大小为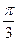 ,求所制作的圆锥形容器容积多少立方米(精确到0. 01m3) (6分)
,求所制作的圆锥形容器容积多少立方米(精确到0. 01m3) (6分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com