
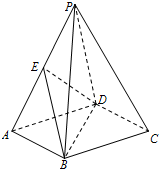
 如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥AD.
如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥AD.分析 (I)连接AC交BD于点O,连接EO.利用中位线定理得出PC∥OE,故而PC∥平面BDE;
(II)证明AD⊥平面PCD,于是BC⊥平面PCD,从而VP-BCD=VB-PCD=$\frac{1}{3}{S}_{△PCD}•BC$.
解答  证明:(Ⅰ)连接AC交BD于点O,连接EO,
证明:(Ⅰ)连接AC交BD于点O,连接EO,
∵四边形ABCD是矩形,
∴O为AC的中点,又E是PA的中点,
∴EO∥PC,又EO?平面BED,PC?平面BED,
∴PC∥平面BED.
(Ⅱ)∵矩形ABCD中,∴AD⊥CD,BC∥AD,
又AD⊥PD,CD?平面PCD,PD?平面PCD,PD∩CD=D,
∴AD⊥平面PCD,
∵BC∥AD,
∴BC⊥平面PCD,
∵CD=1,PC=PD=2,∴${S_{△PCD}}=\frac{1}{2}×1×\sqrt{{2^2}-{{(\frac{1}{2})}^2}}=\frac{{\sqrt{15}}}{4}$,
∴${V_{P-BCD}}={V_{B-PCD}}=\frac{1}{3}×{S_{△PCD}}×BC=\frac{{\sqrt{15}}}{6}$.
点评 本题考查了线面平行的判定,线面垂直的判定,棱锥的体积计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [3.5,+∞) | B. | [1,+∞) | C. | [4,+∞) | D. | [4.5,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的单调减区间是($\frac{2}{3}$,2) | |
| B. | f(x)的极小值是-15 | |
| C. | 当a>2时,对任意的x>2且x≠a,恒有f(x)<f(a)+f′(a)(x-a) | |
| D. | 函数f(x)有且只有两个零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
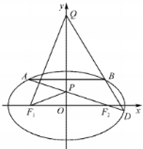 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,且椭圆上一点M与椭圆左右两个焦点构成的三角形周长为4+2$\sqrt{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,且椭圆上一点M与椭圆左右两个焦点构成的三角形周长为4+2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
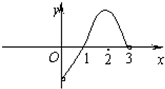 已知函数f(x)是定义在(-3,0)∪(0,3)上的偶函数,当0<x<3时,f(x)的图象如图所示,则不等式f(x)•cosx<0的解集是( )
已知函数f(x)是定义在(-3,0)∪(0,3)上的偶函数,当0<x<3时,f(x)的图象如图所示,则不等式f(x)•cosx<0的解集是( )| A. | (-3,-$\frac{π}{2}$)∪(0,1)∪($\frac{π}{2}$,3) | B. | (-3,-1)∪(-1,0)∪(0,1)∪(1,3) | ||
| C. | (-3,-$\frac{π}{2}$)∪(0,1)∪(1,3) | D. | (-3,-$\frac{π}{2}$)∪(-1,0)∪(0,1)∪($\frac{π}{2}$,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com