
分析 作出函数y=log4x和y=3-x的图象交点A,作出y=($\frac{1}{4}$)x与y=x+3的交点B,y=4x与y=3-x的交点C,根据A,B,C之间的对称关系得出x1,x2的关系.
解答 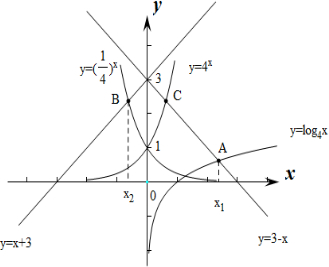 解:当x>0时,令f(x)=0得log4x=3-x,
解:当x>0时,令f(x)=0得log4x=3-x,
作出函数y=log4x和y=3-x的函数图象,设交点为A(x1,y1),
当x<0时,令f(x)=0得($\frac{1}{4}$)x=x+3,
作出函数y=($\frac{1}{4}$)x和y=x+3的函数图象,设交点为B(x2,y2),
显然x1>x2.
作函数y=4x的函数图象,与y=3-x的图象交于C(x0,y0)点.
∵y=($\frac{1}{4}$)x与y=4x的函数图象关于y轴对称,y=x+3与y=3-x的图象关于y轴对称,
∴B,C关于y轴对称,∴x0=-x2,y0=y2,
∵y=4x与y=log4x互为反函数,
∴y=4x与y=log4x的函数图象关于直线y=x对称,又y=3-x关于y=x对称,
∴A,C关于直线y=x对称.∴x0=y1,y0=x1.
∴x2=-y1,
∴|x1-x2|=x1-x2=x1+y1,
又A(x1,y1)在直线y=3-x上,∴x1+y1=3.
故答案为:3.
点评 本题考查了函数基本初等函数的图象,函数零点与函数图象的关系,属于中档题.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②中的X | B. | ①③中的X | C. | ②③中的X | D. | ①②③中的X |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
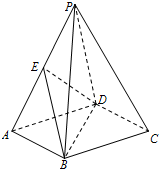 如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥AD.
如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
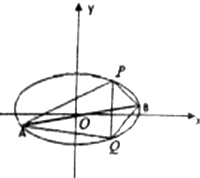 已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧?q | B. | p∧q | C. | ?p∧?q | D. | ?p∧q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com