
| A. | [3.5,+∞) | B. | [1,+∞) | C. | [4,+∞) | D. | [4.5,+∞) |
分析 把函数零点转化为两个函数图象交点的横坐标,根据指数函数与对数函数互为反函数,得到两个函数图象之间的关系求出x1,x2之间的关系,根据两者之和是定值,利用基本不等式得到要求的结果.
解答 解:函数f(x)=ax+x-4的零点是函数y=ax与函数y=4-x图象交点的横坐标,
函数g(x)=logax+x-4的零点是函数y=logax与函数y=4-x图象交点的横坐标,
由于指数函数与对数函数互为反函数,其图象关于直线y=x对称,直线y=4-x与直线y=x垂直,
故直线y=4-x与直线y=x的交点(2,2),∴x1+x2=4,
∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{1}{4}({x}_{1}+{x}_{2})(\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}})$=$\frac{1}{4}(2+\frac{{x}_{1}}{{x}_{2}}+\frac{{x}_{2}}{{x}_{1}})$≥$\frac{1}{4}(2+2\sqrt{\frac{{x}_{1}}{{x}_{2}}•\frac{{x}_{2}}{{x}_{1}}})=1$,
当x1=x2时等号成立,而x1+x2=4,故当x1=x2=2时,$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$≥1,
∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的取值范围是[1,+∞).
故选:B.
点评 本题考查函数零点、反函数的性质,考查利用基本不等式求最值.根据函数图象的对称性找到两个函数零点的关系是解答该题的关键,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②中的X | B. | ①③中的X | C. | ②③中的X | D. | ①②③中的X |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
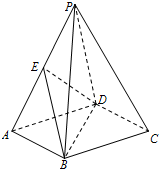 如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥AD.
如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知全集U=R,N={x|$\frac{1}{8}$<2x<1},M={x|y=ln(-x-1)},则图中阴影部分表示的集合是( )
已知全集U=R,N={x|$\frac{1}{8}$<2x<1},M={x|y=ln(-x-1)},则图中阴影部分表示的集合是( )| A. | {x|-3<x<-1} | B. | {x|-3<x<0} | C. | {x|-1≤x<0} | D. | {x|x<-3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com