练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知全集U=R，N={x|$\frac{1}{8}$＜2x＜1}，M={x|y=ln（-x-1）}，则图中阴影部分表示的集合是（　　）
    A．{x|-3＜x＜-1}B．{x|-3＜x＜0}C．{x|-1≤x＜0}D．{x|x＜-3}

    分析 阴影部分用集合表示为N∩CUM，只要求出M、N进行集合的运算即可．

    解答 解：图中阴影部分表示的集合N∩CUM，
    由N={x|$\frac{1}{8}$＜2x＜1}={x|-3＜x＜0}，M={x|y=ln（-x-1）={x|x＜-1}，
    则CUM={x|x≥-1}，
    则N∩CUM={x|-1≤x＜0}．
    故选：C．

    点评 正确理解集合M、N所表达的含义，以及真确理解韦恩图所表达的集合是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．若a＞1，设函数f（x）=ax+x-4的零点是x1，g（x）=logax+x-4的零点为x2，则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的取值范围是（　　）
    A．[3.5，+∞）B．[1，+∞）C．[4，+∞）D．[4.5，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

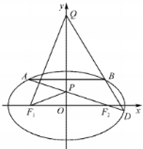    1．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{\sqrt{2}}{2}$，且椭圆上一点M与椭圆左右两个焦点构成的三角形周长为4+2$\sqrt{2}$．
    （1）求椭圆C的方程；
    （2）如图，设点D为椭圆上任意一点，直线y=m和椭圆C交于A、B两点，且直线DA、DB与y轴分别交于P、Q两点，试探究∠PF1F2和∠QF1F2之间的等量关系并加以证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．若x是三角形的最小内角，则函数y=sinx+cosx+sinxcosx的取值范围（1，$\frac{1}{2}+\sqrt{2}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．平面直角坐标系xOy中，椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+y2=1（a＞1）的长轴长为2$\sqrt{2}$，抛物线C2：y2=2px（p＞0）的焦点F是椭圆C1的右焦点．
    （Ⅰ）求椭圆C1与抛物线C2的方程；
    （Ⅱ）过点F作直线l交抛物线C2于A，B两点，射线OA，OB与椭圆C1的交点分别为C，D，若$\overrightarrow{OA}$•$\overrightarrow{OB}$=2$\sqrt{6}$$\overrightarrow{OC}$•$\overrightarrow{OD}$，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

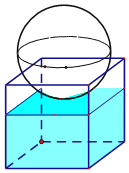    15．如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器注水，当球面恰好接触水面时测得水深为6cm，如不计容器的厚度，则球的表面积为（　　）
    A．100πB．$\frac{500π}{3}$C．50πD．200π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．设O为坐标原点，点A（2，1），若动点M（x，y）满足不等式组$\left\{\begin{array}{l}2x+y-12≤0\\ x-4y+3≤0\\ x≥1\end{array}\right.$，则使$\overrightarrow{OA}•\overrightarrow{OM}$取得最大值的动点M的个数是（　　）
    A．存在唯一1个B．存在无数多个C．恰好2个D．至多存在3个

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

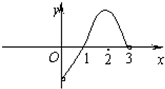    19．已知函数f（x）是定义在（-3，0）∪（0，3）上的偶函数，当0＜x＜3时，f（x）的图象如图所示，则不等式f（x）•cosx＜0的解集是（　　）
    A．（-3，-$\frac{π}{2}$）∪（0，1）∪（$\frac{π}{2}$，3）B．（-3，-1）∪（-1，0）∪（0，1）∪（1，3）
    C．（-3，-$\frac{π}{2}$）∪（0，1）∪（1，3）D．（-3，-$\frac{π}{2}$）∪（-1，0）∪（0，1）∪（$\frac{π}{2}$，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．非零复数z1，z2满足|z1+z2|=|z1-z2|，u=（$\frac{{z}_{1}}{{z}_{2}}$）2，则u（　　）
    A．u＜0B．u＞0C．u=0D．以上都可能

    查看答案和解析>>

    同步练习册答案