练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
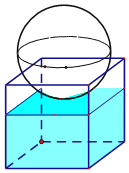
    15．如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器注水，当球面恰好接触水面时测得水深为6cm，如不计容器的厚度，则球的表面积为（　　）
    A．100πB．$\frac{500π}{3}$C．50πD．200π

    分析 设正方体上底面所在平面截球得小圆M，可得圆心M为正方体上底面正方形的中心．设球的半径为R，根据题意得球心到上底面的距离等于（R-2）cm，而圆M的半径为4，由球的截面圆性质建立关于R的方程并解出R即可求出球的表面积．

    解答 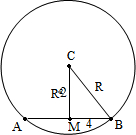解：设正方体上底面所在平面截球得小圆M，
    则圆心M为正方体上底面正方形的中心．如图．
    设球的半径为R，根据题意得球心到上底面的距离等于（R-2）cm，
    而圆M的半径为4，由球的截面圆性质，得R2=（R-2）2+42，
    解得：R=5．
    ∴球的表面积为4π•52=100π．
    故选：A．

    点评 此题主要考查了正方体的性质、垂径定理以及勾股定理等知识，将立体图转化为平面图形是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    5．已知函数f（x）=$\left\{\begin{array}{l}{x+2，x＞a}\\{{x}^{2}+5x+2，x≤a}\end{array}\right.$函数g（x）=f（x）-2x恰有三个不同的零点，则实数a的取值范围是[-1，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数f（x）=sin（2ωx-$\frac{π}{6}}$）-4sin2ωx+2（{ω＞0}），其图象与x轴相邻的两个交点的距离为$\frac{π}{2}$．
    （I）求函数的f（x）解析式；
    （Ⅱ）若将f（x）的图象向左平移m（m＞0）个长度单位得到函数g（x）的图象恰好经过点（${-\frac{π}{3}$，0），求当m取得最小值时，g（x）在[${-\frac{π}{6}$，$\frac{7π}{12}}$]上的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知两条平行直线a、b，a∥平面α，则b与α的位置关系是b?α或b∥α．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知全集U=R，N={x|$\frac{1}{8}$＜2x＜1}，M={x|y=ln（-x-1）}，则图中阴影部分表示的集合是（　　）
    A．{x|-3＜x＜-1}B．{x|-3＜x＜0}C．{x|-1≤x＜0}D．{x|x＜-3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

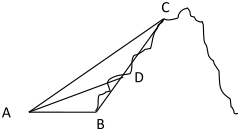    20．如图所示，某旅游景点有一座风景秀丽的山峰，山上有一条笔直的山路BC和一条索道AC，小王和小李打算不坐索道，而是花2个小时的时间进行徒步攀登，已知∠ABC=120°，∠ADC=150°，BD=1（千米），AC=3（千米）．假设小王和小李徒步攀登的速度为每小时1250米，请问：两位登山爱好者能否在2个小时徒步登上山峰．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知公差大于零的等差数列{an}的前n项和为Sn，且满足：a2a4=65，a1+a5=18．
    （1）求数列{an}的通项公式和前n项和Sn．
    （2）设bn=$\frac{n}{（2n+1）Sn}$，数列{bn}的前n项和Tn，证明：Tn＜$\frac{1}{2}$对于任意的正整数n均成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．直角△ABC中，A＜C，且cos（A-C）=sinC，则sinC=$\frac{\sqrt{3}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．下列函数中，既是偶函数又在区间（0，1）上为增函数的是（　　）
    A．y=ln|x|B．y=x-2C．y=x+sinxD．y=cos（-x）

    查看答案和解析>>

    同步练习册答案