
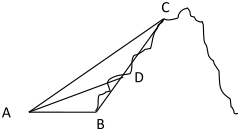
 如图所示,某旅游景点有一座风景秀丽的山峰,山上有一条笔直的山路BC和一条索道AC,小王和小李打算不坐索道,而是花2个小时的时间进行徒步攀登,已知∠ABC=120°,∠ADC=150°,BD=1(千米),AC=3(千米).假设小王和小李徒步攀登的速度为每小时1250米,请问:两位登山爱好者能否在2个小时徒步登上山峰.
如图所示,某旅游景点有一座风景秀丽的山峰,山上有一条笔直的山路BC和一条索道AC,小王和小李打算不坐索道,而是花2个小时的时间进行徒步攀登,已知∠ABC=120°,∠ADC=150°,BD=1(千米),AC=3(千米).假设小王和小李徒步攀登的速度为每小时1250米,请问:两位登山爱好者能否在2个小时徒步登上山峰. 分析 先利用正弦定理,求出AD,再在△ADC中,由余弦定理,求出DC,即可得出结论.
解答 解:在△ABD中,由题意知,∠ADB=∠BAD=30°,∴AB=BD=1,
∵∠ABD=120°,由正弦定理$\frac{AB}{sin∠ADB}=\frac{AD}{sin∠ABD}$,解得$AD=\sqrt{3}$千米,
在△ACD中,由AC2=AD2+CD2-2AD•CD•cos150°,
得$9=3+C{D^2}+2\sqrt{3}×\frac{{\sqrt{3}}}{2}CD$,即CD2+3CD-6=0,$CD=\frac{{\sqrt{33}-3}}{2}$千米,
$BC=BD+CD=\frac{{\sqrt{33}-1}}{2}$千米,
两个小时小王和小李可徒步攀登1250×2=2500米,即2.5千米,
而$\frac{{\sqrt{33}-1}}{2}<\frac{{\sqrt{36}-1}}{2}=\frac{5}{2}=2.5$,
所以两位登山爱好者可以在两个小时内徒步登上山峰.
点评 本题考查解三角形的实际应用,考查正弦定理、余弦定理,考查学生的计算能力,正确运用正弦定理、余弦定理是关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{e}$ | D. | $\frac{1}{2e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m+n>0 | B. | m+n<1 | C. | m+n=1 | D. | m+n>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
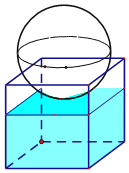 如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的表面积为( )
如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的表面积为( )| A. | 100π | B. | $\frac{500π}{3}$ | C. | 50π | D. | 200π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (-∞,-$\frac{1}{2}$)∪(2,+∞) | C. | (-$\frac{1}{2}$,2) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
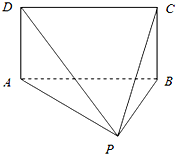 如图,矩形ABCD和△ABP所在的平面互相垂直,AB=2AD=2,PA=PB.
如图,矩形ABCD和△ABP所在的平面互相垂直,AB=2AD=2,PA=PB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 重心 | B. | 垂心 | C. | 外心 | D. | 内心 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$∥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | C. | $\overrightarrow{a}$=$\overrightarrow{b}$ | D. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com