
| A. | 重心 | B. | 垂心 | C. | 外心 | D. | 内心 |
分析 由题意画出图形,根据正弦定理得出|$\overrightarrow{AB}$|sinB=|$\overrightarrow{AC}$|sinC,代入关系式由向量的减法化简,得出$\overrightarrow{AP}$与$\overrightarrow{AD}$共线,由此得出点P的轨迹,从而得出答案.
解答 解:△ABC中,由正弦定理得,$\frac{|\overrightarrow{AC}|}{sinB}$=$\frac{|\overrightarrow{AB}|}{sinC}$,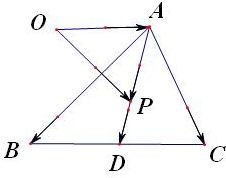 即|$\overrightarrow{AB}$|sinB=|$\overrightarrow{AC}$|sinC,
即|$\overrightarrow{AB}$|sinB=|$\overrightarrow{AC}$|sinC,
设t=|$\overrightarrow{AB}$|sinB,
代入$\overrightarrow{OP}$,则$\overrightarrow{OP}$=$\overrightarrow{OA}$+λt($\overrightarrow{AB}$+$\overrightarrow{AC}$),
∴D是BC的中点,
∴$\overrightarrow{AB}$+$\overrightarrow{AC}$=2$\overrightarrow{AD}$,
∴$\overrightarrow{OP}$=$\overrightarrow{OA}$+2λt$\overrightarrow{AD}$,且λ、t都是常数,
∴$\overrightarrow{AP}$=2λt$\overrightarrow{AD}$,
∴点P的轨迹是直线AD,
∴△ABC的重心一定属于集合M.
故选:A.
点评 本题考查了向量在平面图形中的应用以及正弦定理、向量的减法和共线的应用问题,是综合性题目.


科目:高中数学 来源: 题型:填空题
 如图,在?ABCD中,点E为边AB的中点,BD与CE交于点P,若$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$(x,y∈R),则2x+y=$\frac{5}{3}$;若点Q是△BCP内部(包括边界)一动点,且$\overrightarrow{AQ}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n∈R),则m+2n的取值范围为[1,3].
如图,在?ABCD中,点E为边AB的中点,BD与CE交于点P,若$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$(x,y∈R),则2x+y=$\frac{5}{3}$;若点Q是△BCP内部(包括边界)一动点,且$\overrightarrow{AQ}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n∈R),则m+2n的取值范围为[1,3].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
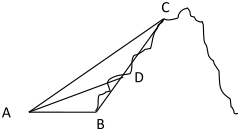 如图所示,某旅游景点有一座风景秀丽的山峰,山上有一条笔直的山路BC和一条索道AC,小王和小李打算不坐索道,而是花2个小时的时间进行徒步攀登,已知∠ABC=120°,∠ADC=150°,BD=1(千米),AC=3(千米).假设小王和小李徒步攀登的速度为每小时1250米,请问:两位登山爱好者能否在2个小时徒步登上山峰.
如图所示,某旅游景点有一座风景秀丽的山峰,山上有一条笔直的山路BC和一条索道AC,小王和小李打算不坐索道,而是花2个小时的时间进行徒步攀登,已知∠ABC=120°,∠ADC=150°,BD=1(千米),AC=3(千米).假设小王和小李徒步攀登的速度为每小时1250米,请问:两位登山爱好者能否在2个小时徒步登上山峰.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin($\frac{1}{3}$x+$\frac{π}{3}$),x∈R | B. | y=sin(3x+$\frac{π}{3}$),x∈R | C. | y=sin(3x+$\frac{π}{9}$),x∈R | D. | y=-sin3x,x∈R |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com