
分析 由题意分析可得,角B为直角,可得A+C=$\frac{π}{2}$,再由cos(A-C)=sinC,得2C-A=$\frac{π}{2}$,联立求得C得答案.
解答 解:在直角△ABC中,A<C,
若C为直角,则由cos(A-C)=sinC,得cos(A-$\frac{π}{2}$)=1,
得sinA=1,A=$\frac{π}{2}$,矛盾;
∴B=$\frac{π}{2}$,则A+C=$\frac{π}{2}$,又cos(A-C)=sinC,得cos(C-A)=sinC,
得C+(C-A)=2C-A=$\frac{π}{2}$,
联立$\left\{\begin{array}{l}{A+C=\frac{π}{2}}\\{2C-A=\frac{π}{2}}\end{array}\right.$,解得C=$\frac{π}{3}$.
∴sinC=sin$\frac{π}{3}=\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查三角函数的化简求值,考查了分类讨论的数学思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
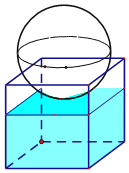 如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的表面积为( )
如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的表面积为( )| A. | 100π | B. | $\frac{500π}{3}$ | C. | 50π | D. | 200π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
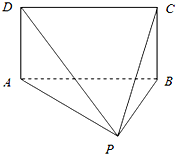 如图,矩形ABCD和△ABP所在的平面互相垂直,AB=2AD=2,PA=PB.
如图,矩形ABCD和△ABP所在的平面互相垂直,AB=2AD=2,PA=PB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
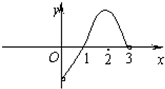 已知函数f(x)是定义在(-3,0)∪(0,3)上的偶函数,当0<x<3时,f(x)的图象如图所示,则不等式f(x)•cosx<0的解集是( )
已知函数f(x)是定义在(-3,0)∪(0,3)上的偶函数,当0<x<3时,f(x)的图象如图所示,则不等式f(x)•cosx<0的解集是( )| A. | (-3,-$\frac{π}{2}$)∪(0,1)∪($\frac{π}{2}$,3) | B. | (-3,-1)∪(-1,0)∪(0,1)∪(1,3) | ||
| C. | (-3,-$\frac{π}{2}$)∪(0,1)∪(1,3) | D. | (-3,-$\frac{π}{2}$)∪(-1,0)∪(0,1)∪($\frac{π}{2}$,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 重心 | B. | 垂心 | C. | 外心 | D. | 内心 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -4 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
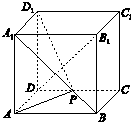 如图,棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )
如图,棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )| A. | DC1⊥D1P | |
| B. | 若直线l是平面ABCD内的直线,直线m是平面DD1C1C内的直线,若l与m相交,则交点一定在直线CD上 | |
| C. | 若P为A1B上动点,则AP+PD1的最小值为$\frac{\sqrt{2}+\sqrt{6}}{2}$ | |
| D. | ∠PAD1最小为$\frac{π}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com