
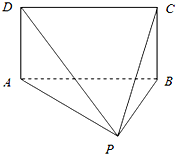
 如图,矩形ABCD和△ABP所在的平面互相垂直,AB=2AD=2,PA=PB.
如图,矩形ABCD和△ABP所在的平面互相垂直,AB=2AD=2,PA=PB.分析 (I)根据面面垂直的性质得出DA⊥平面PAB,故而DA⊥PB;
(II)取AB中点E,则易证PE⊥平面ABCD,故而∠PDE为所求角,根据棱锥的体积求出PE,即可得出tan∠PDE.
解答 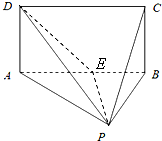 证明:(Ⅰ)∵四边形ABCD是矩形,∴AD⊥AB,
证明:(Ⅰ)∵四边形ABCD是矩形,∴AD⊥AB,
∵平面ABCD⊥平面ABP,平面ABCD∩平面ABP=AB,AD⊥AB,AD?平面ABCD,
∴AD⊥平面ABP,又PB?平面ABP,
∴AD⊥PB.
(Ⅱ)取AB的中点E,连接PE,DE.
∵PA=PB,E是AB的中点,
∴PE⊥AB,
又平面ABCD⊥平面ABP,平面ABCD∩平面ABP=AB,PE?平面ABP,
∴PE⊥平面ABCD,
∴直线PD与平面ABCD所成的角为∠PDE.
∵${{V}_{ABCDP}}={{V}_{P-ABCD}}=\frac{1}{3}×1×2×PE=\frac{2\sqrt{6}}{9}$,∴$PE=\frac{\sqrt{6}}{3}$
∵$DE=\sqrt{A{{E}^{2}}+A{{D}^{2}}}=\sqrt{2}$,∴$tan∠PDE=\frac{PE}{DE}=\frac{\sqrt{3}}{3}$,
∴∠PDE=30°.
所以直线PD与平面ABCD所成的角为30°..
点评 本题考查了面面垂直的性质,棱锥的体积与线面角的计算,属于中档题.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:解答题
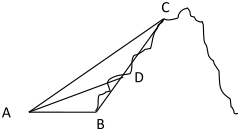 如图所示,某旅游景点有一座风景秀丽的山峰,山上有一条笔直的山路BC和一条索道AC,小王和小李打算不坐索道,而是花2个小时的时间进行徒步攀登,已知∠ABC=120°,∠ADC=150°,BD=1(千米),AC=3(千米).假设小王和小李徒步攀登的速度为每小时1250米,请问:两位登山爱好者能否在2个小时徒步登上山峰.
如图所示,某旅游景点有一座风景秀丽的山峰,山上有一条笔直的山路BC和一条索道AC,小王和小李打算不坐索道,而是花2个小时的时间进行徒步攀登,已知∠ABC=120°,∠ADC=150°,BD=1(千米),AC=3(千米).假设小王和小李徒步攀登的速度为每小时1250米,请问:两位登山爱好者能否在2个小时徒步登上山峰.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin($\frac{1}{3}$x+$\frac{π}{3}$),x∈R | B. | y=sin(3x+$\frac{π}{3}$),x∈R | C. | y=sin(3x+$\frac{π}{9}$),x∈R | D. | y=-sin3x,x∈R |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
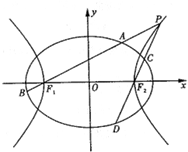 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为$4(\sqrt{2}+1)$.一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为$4(\sqrt{2}+1)$.一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com