
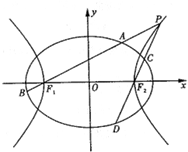
 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为$4(\sqrt{2}+1)$.一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为$4(\sqrt{2}+1)$.一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.分析 (Ⅰ)由椭离心率为$\frac{{\sqrt{2}}}{2}$,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为$4(\sqrt{2}+1)$,求出a,b,从而能求出椭圆的标准方程,设等轴双曲线的标准方程为$\frac{x^2}{m^2}-\frac{y^2}{m^2}=1$,由等轴双曲线的顶点是椭圆的焦点,求出m,从而能求出双曲线的标准方程.
(Ⅱ)设P(x0,y0),F1(-2,0),F2(2,0),则k1=$\frac{y_0}{{{x_0}+2}}$,${k_2}=\frac{y_0}{{{x_0}-2}}$,由此能证明k1k2=1.
(Ⅲ)PF1的方程为y=k1(x+2),将其代入椭圆方程得$({2{k_1}^2+1}){x^2}+8{k_1}^2x+8{k_1}^2-8=0$,由此利用韦达定理、弦长公式,结合已知条件能推导出$\frac{1}{{|{AB}|}}+\frac{1}{{|{CD}|}}$是定值.
解答 解:(Ⅰ)设椭圆的半焦距为c,由题意知:$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,2a+2c=4($\sqrt{2}$+1)
解得a=2$\sqrt{2}$,c=2,
又a2=b2+c2,解得b=2.
故椭圆的标准方程为$\frac{x^2}{8}+\frac{y^2}{4}=1$
由题意设等轴双曲线的标准方程为$\frac{x^2}{m^2}-\frac{y^2}{m^2}=1$(m>0),
因为等轴双曲线的顶点是椭圆的焦点.
所以m=2,
因此双曲线的标准方程为$\frac{x^2}{4}-\frac{y^2}{4}=1$
证明:(Ⅱ)设P(x0,y0),F1(-2,0),F2(2,0)
则k1=$\frac{y_0}{{{x_0}+2}}$,${k_2}=\frac{y_0}{{{x_0}-2}}$.
因为点P在双曲线x2-y2=4上,所以$x_0^2-y_0^2=4$.
因此${k_1}{k_2}=\frac{y_0}{{{x_0}+2}}•\frac{y_0}{{{x_0}-2}}=\frac{y_0^2}{x_0^2-4}=1$,
故k1k2=1.
解:(Ⅲ)设A(x1,y1),B(x2,y2),
由于PF1的方程为y=k1(x+2),将其代入椭圆方程得$({2{k_1}^2+1}){x^2}+8{k_1}^2x+8{k_1}^2-8=0$
所以${x_1}+{x_2}=-\frac{{8{k_1}^2}}{{2{k_1}^2+1}},\;{x_1}•{x_2}=\frac{{8{k_1}^2-8}}{{2{k_1}^2+1}}$,
所以$|{AB}|=\sqrt{1+{k_1}^2}\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}{x_2}}$=$\sqrt{1+{k_1}^2}\sqrt{{{({\frac{{8{k_1}^2}}{{2{k_1}^2+1}}})}^2}-4×\frac{{8{k_1}^2-8}}{{2{k_1}^2+1}}}$=$4\sqrt{2}\frac{{{k_1}^2+1}}{{2{k_1}^2+1}}$
同理可得$|{CD}|=4\sqrt{2}\frac{{{k_2}^2+1}}{{2{k_2}^2+1}}$.
则$\frac{1}{{|{AB}|}}+\frac{1}{{|{CD}|}}=\frac{1}{{4\sqrt{2}}}(\frac{{2{k_1}^2+1}}{{{k_1}^2+1}}+\frac{{2{k_2}^2+1}}{{{k_2}^2+1}})$,
又k1k2=1,
所以$\frac{1}{{|{AB}|}}+\frac{1}{{|{CD}|}}=\frac{1}{{4\sqrt{2}}}(\frac{{2{k_1}^2+1}}{{{k_1}^2+1}}+\frac{{\frac{2}{{{k_1}^2}}+1}}{{\frac{1}{{{k_1}^2}}}})$=$\frac{{\sqrt{2}}}{8}(\frac{{2{k_1}^2+1}}{{{k_1}^2+1}}+\frac{{{k_1}^2+2}}{{{k_1}^2+1}})=\frac{{3\sqrt{2}}}{8}$.
故$\frac{1}{{|{AB}|}}+\frac{1}{{|{CD}|}}=\frac{{3\sqrt{2}}}{8}$恒成立,即$\frac{1}{{|{AB}|}}+\frac{1}{{|{CD}|}}$是定值$\frac{3\sqrt{2}}{8}$.
点评 本题考查椭圆和双曲线的标准方程的求示,考查两直线的斜率之积为1的证明,考查两线段长的倒数和是否为定值的探究,是中档题,解题时要认真审题,注意双曲线、椭圆的性质的合理运用.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:解答题
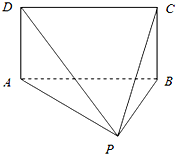 如图,矩形ABCD和△ABP所在的平面互相垂直,AB=2AD=2,PA=PB.
如图,矩形ABCD和△ABP所在的平面互相垂直,AB=2AD=2,PA=PB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$∥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | C. | $\overrightarrow{a}$=$\overrightarrow{b}$ | D. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
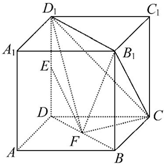 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为线段DD1,BD的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为线段DD1,BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
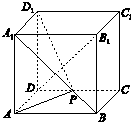 如图,棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )
如图,棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )| A. | DC1⊥D1P | |
| B. | 若直线l是平面ABCD内的直线,直线m是平面DD1C1C内的直线,若l与m相交,则交点一定在直线CD上 | |
| C. | 若P为A1B上动点,则AP+PD1的最小值为$\frac{\sqrt{2}+\sqrt{6}}{2}$ | |
| D. | ∠PAD1最小为$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com