
分析 (1)利用同角三角函数的基本关系式化正弦为余弦,然后利用配方法求最值;
(2)把a=2代入函数解析式,求出函数在x∈[0,$\frac{π}{2}$]上的最大值得答案;
(3)配方后分类求得函数的最小值.
解答 解:(1)当a=2时,f(x)=1-4cosx-2sin2x=1-4cosx-2(1-cos2x)
=2cos2x-4cosx-1=2(cosx-1)2-3,
∵cosx∈[-1,1],∴f(x)∈[-3,5];
(2)当a=2时,f(x)=2(cosx-1)2-3,
∵x∈[0,$\frac{π}{2}$],∴cosx∈[0,1],则cosx∈[-1,0],f(x)∈[-3,-1],
由f(x)≤m恒成立,得m≥-1;
(3)由f(x)=1-2acosx-2sin2x
=1-2acosx-2(1-cos2x)=2cos2x-2acosx-1=$2(cosx-\frac{a}{2})^{2}-\frac{{a}^{2}}{2}-1$,这里-1≤cosx≤1.
①若-1≤$\frac{a}{2}$≤1,则当cosx=$\frac{a}{2}$时,f(x)min=-$\frac{{a}^{2}}{2}$-1;
②若 $\frac{a}{2}$>1,则当cosx=1时,f(x)min=1-2a;
③若 $\frac{a}{2}$<-1,则当cosx=-1时,f(x)min=1+2a.
综上,$g(a)=\left\{\begin{array}{l}{1+2a,a<-2}\\{-\frac{{a}^{2}}{2}-1,-2≤a≤2}\\{1-2a,a>2}\end{array}\right.$.
点评 本题考查三角函数的化简求值,考查了y=Asin(ωx+φ)型函数的图象和性质,是中档题.


科目:高中数学 来源: 题型:解答题
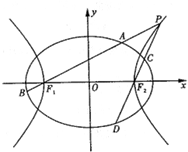 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为$4(\sqrt{2}+1)$.一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为$4(\sqrt{2}+1)$.一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12个 | B. | 10个 | C. | 8个 | D. | 6个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于极轴所在直线对称 | B. | 重合 | ||
| C. | 关于直线$θ=\frac{π}{2}(ρ∈R)$对称 | D. | 关于极点对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 内心 | B. | 外心 | C. | 垂心 | D. | 重心 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com