
| A. | 关于极轴所在直线对称 | B. | 重合 | ||
| C. | 关于直线$θ=\frac{π}{2}(ρ∈R)$对称 | D. | 关于极点对称 |
科目:高中数学 来源: 题型:选择题
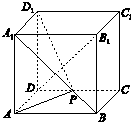 如图,棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )
如图,棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )| A. | DC1⊥D1P | |
| B. | 若直线l是平面ABCD内的直线,直线m是平面DD1C1C内的直线,若l与m相交,则交点一定在直线CD上 | |
| C. | 若P为A1B上动点,则AP+PD1的最小值为$\frac{\sqrt{2}+\sqrt{6}}{2}$ | |
| D. | ∠PAD1最小为$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
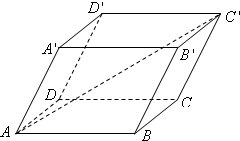 如图,平行六面体ABCD-A′B′C′D′,其中AB=4,AD=3,AA′=3,∠BAD=90°,∠BAA′=60°,∠DAA′=60°,则AC′的长为( )
如图,平行六面体ABCD-A′B′C′D′,其中AB=4,AD=3,AA′=3,∠BAD=90°,∠BAA′=60°,∠DAA′=60°,则AC′的长为( )| A. | $\sqrt{55}$ | B. | $\sqrt{65}$ | C. | $\sqrt{85}$ | D. | $\sqrt{95}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∉(0,+∞),lnx≤x-1 | B. | ¬p:?x∈(0,+∞),lnx≤x-1 | ||
| C. | ¬p:?x∉(0,+∞),lnx≥x-1 | D. | ¬p:?x∈(0,+∞),lnx≤x-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com