
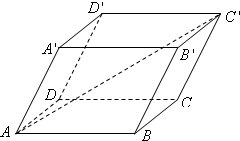
 如图,平行六面体ABCD-A′B′C′D′,其中AB=4,AD=3,AA′=3,∠BAD=90°,∠BAA′=60°,∠DAA′=60°,则AC′的长为( )
如图,平行六面体ABCD-A′B′C′D′,其中AB=4,AD=3,AA′=3,∠BAD=90°,∠BAA′=60°,∠DAA′=60°,则AC′的长为( )| A. | $\sqrt{55}$ | B. | $\sqrt{65}$ | C. | $\sqrt{85}$ | D. | $\sqrt{95}$ |
分析 由$\overrightarrow{A{C}^{′}}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$+$\overrightarrow{A{A}^{′}}$,可得${\overrightarrow{A{C}^{′}}}^{2}$=${\overrightarrow{AB}}^{2}$+${\overrightarrow{AD}}^{2}$+${\overrightarrow{A{A}^{′}}}^{2}$+2$\overrightarrow{AB}•\overrightarrow{AD}$+2$\overrightarrow{AB}•\overrightarrow{A{A}^{′}}$+2$\overrightarrow{AD}•\overrightarrow{A{A}^{′}}$,再利用数量积运算性质即可得出.
解答 解:${\overrightarrow{AB}}^{2}$=16,${\overrightarrow{AD}}^{2}$=9,${\overrightarrow{A{A}^{′}}}^{2}$=9,$\overrightarrow{AB}•\overrightarrow{AD}$=4×3×cos90°=0,
$\overrightarrow{AB}•\overrightarrow{A{A}^{′}}$=4×3×cos60°=6,$\overrightarrow{AD}•\overrightarrow{A{A}^{′}}$=3×3×cos60°=$\frac{9}{2}$.
∵$\overrightarrow{A{C}^{′}}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$+$\overrightarrow{A{A}^{′}}$,
∴${\overrightarrow{A{C}^{′}}}^{2}$=${\overrightarrow{AB}}^{2}$+${\overrightarrow{AD}}^{2}$+${\overrightarrow{A{A}^{′}}}^{2}$+2$\overrightarrow{AB}•\overrightarrow{AD}$+2$\overrightarrow{AB}•\overrightarrow{A{A}^{′}}$+2$\overrightarrow{AD}•\overrightarrow{A{A}^{′}}$
=16+9+9+2×0+2×6+2×$\frac{9}{2}$=55,
∴$|\overrightarrow{A{C}^{′}}|$=$\sqrt{55}$,
故选:A.
点评 本题考查了向量的平行六面体法则、数量积运算性质,考查了推理能力与计算能力,属于中档题.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于极轴所在直线对称 | B. | 重合 | ||
| C. | 关于直线$θ=\frac{π}{2}(ρ∈R)$对称 | D. | 关于极点对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | [1,2] | C. | [1,2) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 内心 | B. | 外心 | C. | 垂心 | D. | 重心 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+i | B. | 1-i | C. | -1-i | D. | -i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com