
分析 (I)a<-1,f(x)=|x3-1|+x3+ax=$\left\{\begin{array}{l}{2{x}^{3}+ax-1,x≥1}\\{ax+1,x<1}\end{array}\right.$,分类讨论,再利用导数研究函数的单调性,从而求得求得它的最小值.
(Ⅱ)证明x1x2>1,即可证明f(x1x2)>f(1)=a+1.
解答 解:(I)∵a<-1,f(x)=|x3-1|+x3+ax=$\left\{\begin{array}{l}{2{x}^{3}+ax-1,x≥1}\\{ax+1,x<1}\end{array}\right.$,
若-$\frac{a}{6}$≥1,即a≤-6时,则当x>1时,f(x)=2x3+ax-1,f′(x)=6x2+a,令f′(x)=0,求得x=$\sqrt{-\frac{a}{6}}$.
故在(1,$\sqrt{-\frac{a}{6}}$)上,f′(x)<0,f(x)单调递减;
在( $\sqrt{-\frac{a}{6}}$,+∞)上,f′(x)>0,f(x)单调递增.
当x<1时,函数f(x)=ax+1,函数单调递减,故f(x)在(-∞,$\sqrt{-\frac{a}{6}}$)上单调递减,
在($\sqrt{-\frac{a}{6}}$,+∞)上单调递增,
故函数f(x)的最小值为f($\sqrt{-\frac{a}{6}}$)=$\frac{2}{3}$a•$\sqrt{-\frac{a}{6}}$-1.
若-$\frac{a}{6}$<1,即-1>a>-6时,
则当x>1时,f(x)=2x3+ax-1,f′(x)=6x2+a,在(1,+∞)上,f′(x)>0,f(x)单调递增.
当x<1时,函数f(x)=ax+1,函数单调递减,
故f(x)在(-∞,1)上单调递减,在(1,+∞)上单调递增,
故f(x)的最小值为f(1)=1+a.
综上可得,fmin(x)=$\left\{\begin{array}{l}{\frac{2a}{3}•\sqrt{-\frac{a}{6}}-1,a≤-6}\\{1+a,-6<a<-1}\end{array}\right.$.
(Ⅱ)若函数f(x)有两个零点x1,x2,不妨令x1<x2,
则x1=-$\frac{1}{a}$∈($\frac{1}{6}$,1),x2>1,
x2-$\frac{1}{{x}_{1}}$=x2+a=x2+$\frac{1}{{x}_{2}}$+$2{{x}_{2}}^{2}$,
令y=x+$\frac{1}{x}$+2x2,y′=1-$\frac{1}{{x}^{2}}$+4x>0,∴函数在(1,+∞)上单调递增,
∴y>4>0,
∴x2-$\frac{1}{{x}_{1}}$>0,
∴x1x2>1,
故f(x1x2)>f(1)=a+1.
点评 本题考查的知识点是分段函数的应用,分类讨论思想,函数的零点,本题转化复杂,运算量大,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -4 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
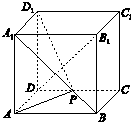 如图,棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )
如图,棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )| A. | DC1⊥D1P | |
| B. | 若直线l是平面ABCD内的直线,直线m是平面DD1C1C内的直线,若l与m相交,则交点一定在直线CD上 | |
| C. | 若P为A1B上动点,则AP+PD1的最小值为$\frac{\sqrt{2}+\sqrt{6}}{2}$ | |
| D. | ∠PAD1最小为$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
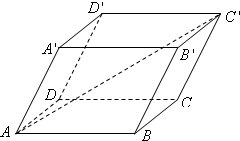 如图,平行六面体ABCD-A′B′C′D′,其中AB=4,AD=3,AA′=3,∠BAD=90°,∠BAA′=60°,∠DAA′=60°,则AC′的长为( )
如图,平行六面体ABCD-A′B′C′D′,其中AB=4,AD=3,AA′=3,∠BAD=90°,∠BAA′=60°,∠DAA′=60°,则AC′的长为( )| A. | $\sqrt{55}$ | B. | $\sqrt{65}$ | C. | $\sqrt{85}$ | D. | $\sqrt{95}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com