
分析 (1)利用a1+a5=a2+a4=18可求出a2,a4,再列方程解出首项和公差,继而得出通项公式和前n项和公式;
(2)化简得bn=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),然后使用裂项法求出Tn即可得出结论.
解答 解:(1)数列{an}为等差数列,因为a1+a5=a2+a4=18,
又a2a4=65,∴a2,a4是方程x2-18x+65=0的两个根,
又公差d>0,∴a2<a4,∴a2=5,a4=13.
∴$\left\{\begin{array}{l}{{a}_{1}+d=5}\\{{a}_{1}+3d=13}\end{array}\right.$,解得a1=1,d=4.
∴an=4n-3.
Sn=n×1+$\frac{n(n-1)}{2}$×4=2n2-n,
(2)由(1)知,Sn=2n2-n,
∴bn=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$).
∴Tn=b1+b2+…+bn
=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)<$\frac{1}{2}$,
∴Tn<$\frac{1}{2}$对于任意的正整数n均成立.
点评 本题考查了等差数列的性质,裂项法数列求和,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | f(x)的单调减区间是($\frac{2}{3}$,2) | |
| B. | f(x)的极小值是-15 | |
| C. | 当a>2时,对任意的x>2且x≠a,恒有f(x)<f(a)+f′(a)(x-a) | |
| D. | 函数f(x)有且只有两个零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
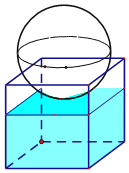 如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的表面积为( )
如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的表面积为( )| A. | 100π | B. | $\frac{500π}{3}$ | C. | 50π | D. | 200π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在唯一1个 | B. | 存在无数多个 | C. | 恰好2个 | D. | 至多存在3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
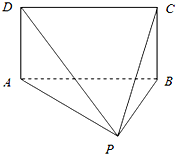 如图,矩形ABCD和△ABP所在的平面互相垂直,AB=2AD=2,PA=PB.
如图,矩形ABCD和△ABP所在的平面互相垂直,AB=2AD=2,PA=PB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
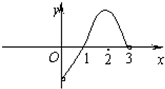 已知函数f(x)是定义在(-3,0)∪(0,3)上的偶函数,当0<x<3时,f(x)的图象如图所示,则不等式f(x)•cosx<0的解集是( )
已知函数f(x)是定义在(-3,0)∪(0,3)上的偶函数,当0<x<3时,f(x)的图象如图所示,则不等式f(x)•cosx<0的解集是( )| A. | (-3,-$\frac{π}{2}$)∪(0,1)∪($\frac{π}{2}$,3) | B. | (-3,-1)∪(-1,0)∪(0,1)∪(1,3) | ||
| C. | (-3,-$\frac{π}{2}$)∪(0,1)∪(1,3) | D. | (-3,-$\frac{π}{2}$)∪(-1,0)∪(0,1)∪($\frac{π}{2}$,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -4 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com