
分析 化简g(x)=f(x)-2x=$\left\{\begin{array}{l}{-x+2,x>a}\\{{x}^{2}+3x+2,x≤a}\end{array}\right.$,而方程-x+2=0的解为2,方程x2+3x+2=0的解为-1,-2;故只需$\left\{\begin{array}{l}{a<2}\\{-1≤a}\\{-2≤a}\end{array}\right.$,从而可得答案.
解答 解:∵f(x)=$\left\{\begin{array}{l}{x+2,x>a}\\{{x}^{2}+5x+2,x≤a}\end{array}\right.$,
∴g(x)=f(x)-2x=$\left\{\begin{array}{l}{-x+2,x>a}\\{{x}^{2}+3x+2,x≤a}\end{array}\right.$,
而方程-x+2=0的解为2,方程x2+3x+2=0的解为-1,-2;
若函数g(x)=f(x)-2x恰有三个不同的零点,
则$\left\{\begin{array}{l}{a<2}\\{-1≤a}\\{-2≤a}\end{array}\right.$,
解得-1≤a<2,
即实数a的取值范围是[-1,2).
故答案为:[-1,2).
点评 本题考查了分段函数的化简与函数零点的判断,属于中档题.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 16 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长是短轴长的两倍,焦距为2$\sqrt{3}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长是短轴长的两倍,焦距为2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3.5,+∞) | B. | [1,+∞) | C. | [4,+∞) | D. | [4.5,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{e}$ | D. | $\frac{1}{2e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的单调减区间是($\frac{2}{3}$,2) | |
| B. | f(x)的极小值是-15 | |
| C. | 当a>2时,对任意的x>2且x≠a,恒有f(x)<f(a)+f′(a)(x-a) | |
| D. | 函数f(x)有且只有两个零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
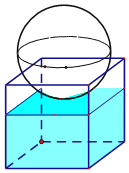 如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的表面积为( )
如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的表面积为( )| A. | 100π | B. | $\frac{500π}{3}$ | C. | 50π | D. | 200π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com