
分析 (Ⅰ)由已知可得:2a=2$\sqrt{2}$,b=1,c=$\sqrt{{a}^{2}-{b}^{2}}$,解出即可得出椭圆C1的方程.利用$\frac{p}{2}$=c,解得p,即可得出抛物线C2的方程.
(Ⅱ)设直线l的方程为:x=my+1,A$(\frac{{y}_{1}^{2}}{4},{y}_{1})$,B$(\frac{{y}_{2}^{2}}{4},{y}_{2})$,C(x3,y3),D(x4,y4).直线方程与抛物线方程联立可得:y2-my-4=0,利用斜率计算公式可得kOA,进而定点直线OA的方程,与椭圆方程联立可得$(\frac{{y}_{1}^{2}}{16}+2){y}^{2}$=2,进而得到${y}_{3}^{2}$,${y}_{4}^{2}$,利用向量数量积运算性质可得:$\overrightarrow{OA}•\overrightarrow{OB}$,$\overrightarrow{OC}•\overrightarrow{OD}$,利用$\overrightarrow{OA}$•$\overrightarrow{OB}$=2$\sqrt{6}$$\overrightarrow{OC}$•$\overrightarrow{OD}$,及其根与系数的关系解出m,即可得出.
解答 解:(Ⅰ)由已知可得:2a=2$\sqrt{2}$,b=1,c=$\sqrt{{a}^{2}-{b}^{2}}$,
解得a=$\sqrt{2}$,b=c=1.
∴椭圆C1的方程为:$\frac{{x}^{2}}{2}+{y}^{2}$=1.
又F(1,0),∴$\frac{p}{2}$=1,解得p=2.
∴抛物线C2的方程为y2=4x.
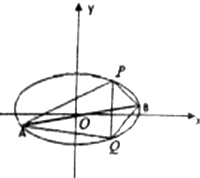
(Ⅱ)设直线l的方程为:x=my+1,A$(\frac{{y}_{1}^{2}}{4},{y}_{1})$,B$(\frac{{y}_{2}^{2}}{4},{y}_{2})$,C(x3,y3),D(x4,y4).
联立$\left\{\begin{array}{l}{x=my+1}\\{{y}^{2}=4x}\end{array}\right.$,化为:y2-my-4=0,∴y1+y2=4m,y1•y2=-4.
△=16m2+16>0,
∴kOA=$\frac{{y}_{1}}{\frac{{y}_{1}^{2}}{4}}$=$\frac{4}{{y}_{1}}$,∴直线OA的方程为:x=$\frac{{y}_{1}}{4}$y,
∴$\left\{\begin{array}{l}{4x={y}_{1}y}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$,得$(\frac{{y}_{1}^{2}}{16}+2){y}^{2}$=2,${y}_{3}^{2}$=$\frac{32}{{y}_{1}^{2}+32}$,同理${y}_{4}^{2}$=$\frac{32}{{y}_{2}^{2}+32}$,
∴$\overrightarrow{OA}•\overrightarrow{OB}$=$\frac{{y}_{1}^{2}}{4}$×$\frac{{y}_{2}^{2}}{4}$+y1y2=-3,
$\overrightarrow{OC}•\overrightarrow{OD}$=x3x4+y3y4=$\frac{{y}_{1}}{4}{y}_{3}•\frac{{y}_{2}}{4}{y}_{4}$+y3y4=$\frac{3}{4}$y3y4,
∵$\overrightarrow{OA}$•$\overrightarrow{OB}$=2$\sqrt{6}$$\overrightarrow{OC}$•$\overrightarrow{OD}$,∴y3y4=-$\frac{\sqrt{6}}{3}$,
∴${y}_{3}^{2}{y}_{4}^{2}$=$\frac{32}{{y}_{1}^{2}+32}$•$\frac{32}{{y}_{2}^{2}+32}$=$\frac{3{2}^{2}}{({y}_{1}{y}_{2})^{2}+32({y}_{1}^{2}+{y}_{2}^{2})+3{2}^{2}}$=$\frac{64}{32{m}^{2}+81}$=$(-\frac{\sqrt{6}}{3})^{2}$,
∴m2=$\frac{15}{32}$,∴m=$±\frac{\sqrt{30}}{8}$,∴直线l的方程为:x=±$\frac{\sqrt{30}}{8}$y+1.
点评 本题考查了抛物线与椭圆的标准方程及其性质、直线与抛物线椭圆相交问题、一元二次方程的根与系数的关系、向量数量积运算性质,考查了推理能力与计算能力,属于难题.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | ①②中的X | B. | ①③中的X | C. | ②③中的X | D. | ①②③中的X |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知全集U=R,N={x|$\frac{1}{8}$<2x<1},M={x|y=ln(-x-1)},则图中阴影部分表示的集合是( )
已知全集U=R,N={x|$\frac{1}{8}$<2x<1},M={x|y=ln(-x-1)},则图中阴影部分表示的集合是( )| A. | {x|-3<x<-1} | B. | {x|-3<x<0} | C. | {x|-1≤x<0} | D. | {x|x<-3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧?q | B. | p∧q | C. | ?p∧?q | D. | ?p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2019,2017} | B. | {-2015} | C. | {0,2017,-2018} | D. | {2017,2019,-2015} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com