
 ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������e=$\frac{\sqrt{2}}{2}$������Բ��һ��M����Բ�����������㹹�ɵ��������ܳ�Ϊ4+2$\sqrt{2}$��
��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������e=$\frac{\sqrt{2}}{2}$������Բ��һ��M����Բ�����������㹹�ɵ��������ܳ�Ϊ4+2$\sqrt{2}$������ ��1����������ɵã�e=$\frac{\sqrt{2}}{2}$=$\frac{c}{a}$��2a+2c=4+2$\sqrt{2}$����a2=b2+c2������������ɵó���ԲC�ķ��̣�
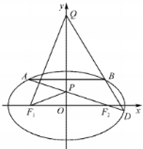
��2����D��x0��y0������$\frac{{x}_{0}^{2}}{4}$+$\frac{{y}_{0}^{2}}{2}$=1����y=m������Բ���̿ɵã�A��-$\sqrt{4-2{m}^{2}}$��m����B��$\sqrt{4-2{m}^{2}}$��m�������õ�бʽ�ɵã�ֱ��DA�ķ�����ֱ��DB�ķ��̣��ɵ�P��Q�����꣮����б�ʹ�ʽֻҪ֤��${k}_{P{F}_{1}}$•${k}_{Q{F}_{1}}$=1���ɵó���
��� ��1���⣺������ɵã�e=$\frac{\sqrt{2}}{2}$=$\frac{c}{a}$��2a+2c=4+2$\sqrt{2}$����a2=b2+c2��
������ã�a=2��b=c=$\sqrt{2}$��
����ԲC�ķ���Ϊ��$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}$=1��
��2���⣺��PF1F2+��QF1F2=90�㣮
�������֤����F1$��-\sqrt{2}��0��$��
��D��x0��y0������$\frac{{x}_{0}^{2}}{4}$+$\frac{{y}_{0}^{2}}{2}$=1��
��y=m������Բ���̿ɵã�$\frac{{x}^{2}}{4}$+$\frac{{m}^{2}}{2}$=1�����x=��$\sqrt{4-2{m}^{2}}$��
ȡA��-$\sqrt{4-2{m}^{2}}$��m����B��$\sqrt{4-2{m}^{2}}$��m����
ֱ��DA�ķ���Ϊ��y-y0=$\frac{m-{y}_{0}}{-\sqrt{4-2{m}^{2}}-{x}_{0}}$��x-x0�����ɵ�P$��0��\frac{��m-{y}_{0}��{x}_{0}}{\sqrt{4-2{m}^{2}}+{x}_{0}}+{y}_{0}��$��
ͬ���ɵã�ֱ��DB�ķ���Ϊ��y-y0=$\frac{m-{y}_{0}}{\sqrt{4-2{m}^{2}}-{x}_{0}}$��x-x0�����ɵ�Q$��0��\frac{-{x}_{0}��m-{y}_{0}��}{\sqrt{4-2{m}^{2}}-{x}_{0}}+{y}_{0}��$��
��${k}_{P{F}_{1}}$=$\frac{m{x}_{0}+{y}_{0}\sqrt{4-2{m}^{2}}}{\sqrt{2}��\sqrt{4-2{m}^{2}}+{x}_{0}��}$��
${k}_{Q{F}_{1}}$=$\frac{-m{x}_{0}+{y}_{0}\sqrt{4-2{m}^{2}}}{\sqrt{2}��\sqrt{4-2{m}^{2}}-{x}_{0}��}$��
��${y}_{0}^{2}$=2-$\frac{{x}_{0}^{2}}{2}$��
��${k}_{P{F}_{1}}$•${k}_{Q{F}_{1}}$=$\frac{m{x}_{0}+{y}_{0}\sqrt{4-2{m}^{2}}}{\sqrt{2}��\sqrt{4-2{m}^{2}}+{x}_{0}��}$•$\frac{-m{x}_{0}+{y}_{0}\sqrt{4-2{m}^{2}}}{\sqrt{2}��\sqrt{4-2{m}^{2}}-{x}_{0}��}$=$\frac{{y}_{0}^{2}��4-2{m}^{2}��-{m}^{2}{x}_{0}^{2}}{2��4-2{m}^{2}-{x}_{0}^{2}��}$=$\frac{��2-\frac{{x}_{0}^{2}}{2}����4-2{m}^{2}��-{m}^{2}{x}_{0}^{2}}{2��4-2{m}^{2}-{x}_{0}^{2}��}$=1��
���PF1F2+��QF1F2=90�㣮
���� ���⿼������Բ�ı����̼������ʡ�ֱ������Բ�ཻ���⡢ֱ�߷��̡�б�ʼ��㹫ʽ��������Բ��λ�ù�ϵ��������̽����������������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
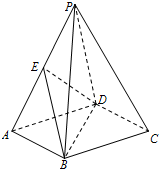 ��ͼ����������P-ABCD�У�����ABCD�Ǿ��Σ�E����PA���е㣬PD��AD��
��ͼ����������P-ABCD�У�����ABCD�Ǿ��Σ�E����PA���е㣬PD��AD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30�� | B�� | 45�� | C�� | 60�� | D�� | 75�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
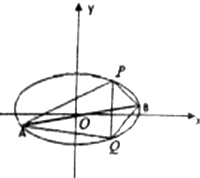 ��֪��ԲC��������ԭ�㣬������x���ϣ�������Ϊ$\frac{1}{2}$������һ������ǡ����������x2=8$\sqrt{3}$y�Ľ��㣮
��֪��ԲC��������ԭ�㣬������x���ϣ�������Ϊ$\frac{1}{2}$������һ������ǡ����������x2=8$\sqrt{3}$y�Ľ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��֪ȫ��U=R��N={x|$\frac{1}{8}$��2x��1}��M={x|y=ln��-x-1��}����ͼ����Ӱ���ֱ�ʾ�ļ����ǣ�������
��֪ȫ��U=R��N={x|$\frac{1}{8}$��2x��1}��M={x|y=ln��-x-1��}����ͼ����Ӱ���ֱ�ʾ�ļ����ǣ�������| A�� | {x|-3��x��-1} | B�� | {x|-3��x��0} | C�� | {x|-1��x��0} | D�� | {x|x��-3} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com