
分析 (Ⅰ)由正弦定理,三角函数恒等变换的应用化简已知可得sin(B-$\frac{π}{6}$)=1,结合B的范围即可得解B的值.
(Ⅱ)由已知利用三角形面积公式可求ac=2,由余弦定理可得:a2+c2=5,联立即可求得a,c的值.
解答 (本题满分为12分)
解:(Ⅰ)∵$\sqrt{3}$bsinA-acosB-2a=0.
∴由正弦定理可得:$\sqrt{3}$sinBsinA-sinAcosB-2sinA=0,
∴$\sqrt{3}$sinB-cosB=2,可得sin(B-$\frac{π}{6}$)=1,
∵B∈(0,π),B-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{5π}{6}$),可得:B-$\frac{π}{6}$=$\frac{π}{2}$,
∴B=$\frac{2π}{3}$…6分
(Ⅱ)∵△ABC的面积为$\frac{\sqrt{3}}{2}$=$\frac{1}{2}$acsinB=$\frac{1}{2}$acsin$\frac{2π}{3}$,
∴ac=2,①
∵b=$\sqrt{7}$,B=$\frac{2π}{3}$,由余弦定理可得:a2+c2-2accos$\frac{2π}{3}$=7,解得:a2+c2=5,②
∴联立①②可得:a=1,c=2,或a=2,c=1…12分
点评 本题主要考查了正弦定理,三角函数恒等变换的应用,三角形面积公式,余弦定理在解三角形中的综合应用,考查了计算能力和转化思想,属于基础题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x-4=0,则x=4”的逆否命题为“若x≠4,则x2-3x-4=0” | |
| B. | 已知命题p“若m>0,则方程x2+x-m=0有实根”,则命题p的否定¬p为真命题 | |
| C. | “x=4”是“x2-3x-4=0”的充分不必要条件 | |
| D. | 命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2=0,则m≠0或n≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
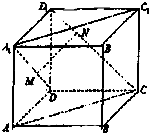 如图,正方形ABCD-A1B1C1D1的棱长为3,在面对角线A1D上取点M,在面对角线C1D上取点N,使得MN∥平面AA1C1C,当线段MN长度取到最小值时,三棱锥A1-MND1的体积为1.
如图,正方形ABCD-A1B1C1D1的棱长为3,在面对角线A1D上取点M,在面对角线C1D上取点N,使得MN∥平面AA1C1C,当线段MN长度取到最小值时,三棱锥A1-MND1的体积为1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2018 | B. | -2019 | C. | 2019 | D. | 2018 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {-1,0,1} | C. | {0,1,5} | D. | {-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
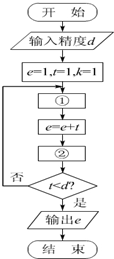 用e≈1+$\frac{1}{1!}$+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{n!}$求e的近似值(n!=1×2×3×…×n),流程图如图所示.在①、②处分别填上适当的式子.①$t=\frac{t}{k}$,②k=k+1.
用e≈1+$\frac{1}{1!}$+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{n!}$求e的近似值(n!=1×2×3×…×n),流程图如图所示.在①、②处分别填上适当的式子.①$t=\frac{t}{k}$,②k=k+1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com