
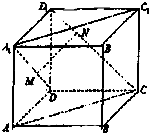
 如图,正方形ABCD-A1B1C1D1的棱长为3,在面对角线A1D上取点M,在面对角线C1D上取点N,使得MN∥平面AA1C1C,当线段MN长度取到最小值时,三棱锥A1-MND1的体积为1.
如图,正方形ABCD-A1B1C1D1的棱长为3,在面对角线A1D上取点M,在面对角线C1D上取点N,使得MN∥平面AA1C1C,当线段MN长度取到最小值时,三棱锥A1-MND1的体积为1. 分析 MN长度最小值,做平面A1BD和CB1D1,对角线平行,故平面A1BD∥平面CB1D1.要使MN长度取到最小值,即最小值为两平面之间的距离,确定M,N的位置,根据相似A1-MND1求边长,即可求解三棱锥A1-MND1的体积.
解答 解:如图:MN长度最小值,做平面A1BD和CB1D1,对角线平行,故平面A1BD∥平面CB1D1.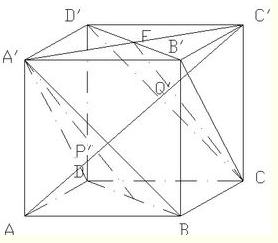
∴动点M,N,要使MN长度取到最小值,即最小值为两平面之间的距离,且MN∥平面AA1C1C,
易证AC1⊥面A1BD,AC1⊥面A1BDC,AC1与两平面分布交于P1Q1,又∵在A1C1P1中,PQ1为中线,
∴P1Q1=AP1
所以:P1Q1=$\frac{1}{3}$AC1
P1Q1∥平面AA1C1C,故而MN∥平面AA1C1C,
又∵P1Q1=$\frac{1}{3}$AC1,可知M,N在A1D,CD1的长度的$\frac{1}{3}$处.
那么:${S}_{△{A}_{1}}M{D}_{1}=\frac{1}{2}×\frac{2}{3}{A}_{1}D×\frac{1}{2}A{D}_{1}$=3.
N在DD1的长度为$\frac{1}{3}$CD.
∴三棱锥A1-MND1的体积V=$\frac{1}{3}×{S}_{{A}_{1}M{D}_{1}}×\frac{1}{3}CD=1$
点评 本题考察了动点的变化,两点直线的动点问题,可以转化为平面的之间的最短距离来考虑.由相似比例求其位置,在求其体积.属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | (-∞,2] | C. | (-∞,-1)和(1,2) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com