
| A. | [-1,+∞) | B. | (-∞,2] | C. | (-∞,-1)和(1,2) | D. | [2,+∞) |
分析 由切线方程y-y0=(x0-2)(x02-1)(x-x0),可知任一点的导数为f′(x)=(x-2)(x2-1),然后由f′(x)<0,可求单调递减区间.
解答 解:因为函数f(x),(x∈R)上任一点(x0y0)的切线方程为y-y0=(x0-2)(x02-1)(x-x0),
即函数在任一点(x0y0)的切线斜率为k=(x0-2)(x02-1),即知任一点的导数为f′(x)=(x-2)(x2-1).
由f′(x)=(x-2)(x2-1)<0,得x<-1或1<x<2,即函数f(x)的单调递减区间是(-∞,-1)和(1,2).
故选C.
点评 本题的考点是利用导数研究函数的单调性,先由切线方程得到切线斜率,进而得到函数的导数,然后解导数不等式,是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $(-∞\;,\;ln(\sqrt{2}+1)]$ | B. | $[ln(\sqrt{2}-1)\;,\;+∞)$ | ||
| C. | $[ln(\sqrt{2}-1)\;,\;ln(\sqrt{2}+1)]$ | D. | $(-∞\;,\;ln(\sqrt{2}-1)]∪$$[ln(\sqrt{2}+1)\;,\;+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x-4=0,则x=4”的逆否命题为“若x≠4,则x2-3x-4=0” | |
| B. | 已知命题p“若m>0,则方程x2+x-m=0有实根”,则命题p的否定¬p为真命题 | |
| C. | “x=4”是“x2-3x-4=0”的充分不必要条件 | |
| D. | 命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2=0,则m≠0或n≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
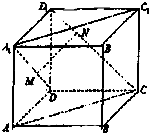 如图,正方形ABCD-A1B1C1D1的棱长为3,在面对角线A1D上取点M,在面对角线C1D上取点N,使得MN∥平面AA1C1C,当线段MN长度取到最小值时,三棱锥A1-MND1的体积为1.
如图,正方形ABCD-A1B1C1D1的棱长为3,在面对角线A1D上取点M,在面对角线C1D上取点N,使得MN∥平面AA1C1C,当线段MN长度取到最小值时,三棱锥A1-MND1的体积为1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {-1,0,1} | C. | {0,1,5} | D. | {-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1008×1009 | B. | 1007×1008 | C. | 1005×1004 | D. | 1006×1005 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com