
| A. | (-∞,1) | B. | (-∞,-1) | C. | (-1,+∞) | D. | (1,+∞) |
分析 利用函数f(x)=x3+x是奇函数又是[0,$\frac{π}{2}$]上的增函数,把不等式转化求解.
解答 解:∵函数f(x)=x3+x是奇函数又是(0,$\frac{π}{2}$]上的增函数,
∴f(mcosθ)+f(1-m)>0恒成立,等价于f(mcosθ)>-f(1-m)
即f(mcosθ)>f(m-1)即mcosθ>m-1⇒m<$\frac{1}{1-cosθ}$,
又0<θ≤$\frac{π}{2}$时,0≤cosθ<1,
即有$\frac{1}{1-cosθ}$≥1,
∴m<1.
故选:A.
点评 考查函数的奇偶性单调性的综合运用以及三角函数的单调性的运用能力,属中档题.


科目:高中数学 来源: 题型:解答题
| 分数(分数段) | 频数(人数) | 频率 |
| [60,70) | 9 | x |
| [70,80) | y | 0.38 |
| [80,90) | 16 | 0.32 |
| [90,100) | z | s |
| 合计 | p | 1 |
查看答案和解析>>
科目:高中数学 来源:2017届安徽淮北十二中高三上月考二数学(理)试卷(解析版) 题型:选择题
函数 是定义在实数集
是定义在实数集 上的奇函数,且当
上的奇函数,且当 时,
时, 成立,若
成立,若 ,则
,则 大小关系( )
大小关系( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2011 | B. | $\frac{2011}{2}$ | C. | 22011 | D. | 2-2011 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
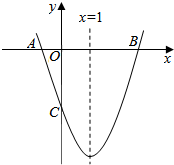 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高二上理周末检测三数学试卷(解析版) 题型:选择题
在 中,内角
中,内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,且
,且 边上的高为
边上的高为 ,则
,则 的最大值为( )
的最大值为( )
A. B.
B.
C. D.4
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com