Question

【题目】某校某次N名学生的学科能力测评成绩（满分120分）的频率分布直方图如下，已知分数在100﹣110的学生数有21人
（1）求总人数N和分数在110﹣115分的人数n．；
（2）现准备从分数在110﹣115的n名学生（女生占 ）中选3位分配给A老师进行指导，设随机变量ξ表示选出的3位学生中女生的人数，求ξ的分布列与数学期望Eξ；
（3）为了分析某个学生的学习状态，对其下一阶段的学习提供指导建议，对他前7次考试的数学成绩x、物理成绩y进行分析，该生7次考试成绩如表

数学（x）	88	83	117	92	108	100	112
物理（y）	94	91	108	96	104	101	106

已知该生的物理成绩y与数学成绩x是线性相关的，求出y关于x的线性回归方程 = x+ ．若该生的数学成绩达到130分，请你估计他的物理成绩大约是多少？
附：对于一组数据（x1 ， y1），（x2 ， y2），…，（xn ， yn），其回归方程 = x+ 的斜率和截距的最小二乘估计分别为 = ， ．

Answer 1

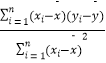【答案】
（1）解：分数在100﹣110内的学生的频率为P1=（0.04+0.03）×5=0.35，

所以该班总人数为N= =60，

分数在110﹣115内的学生的频率为

P2=1﹣（0.01+0.04+0.05+0.04+0.03+0.01）×5=0.1，

分数在110﹣115内的人数为n=60×0.1=6

（2）解：由题意分数在110﹣115内有6名学生，其中女生有2名，

从6名学生中选出3人，女生人数ξ的可能取值为0，1，2；

则P（ξ=0）= = ，P（ξ=1）= = ，P（ξ=2）= = ；

所以ξ的分布列为：

ξ	0	1	2
P

ξ的数学期望为Eξ=0× +1× +2× =1

（3）解：计算 = ×（88+83+117+92+108+100+112）=100，

= ×（94+91+108+96+104+101+106）=100；

由于x与y之间具有线性相关关系，

根据回归系数公式得到 = = 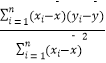=0.5，

=100﹣0.5×100=50，

∴线性回归方程为 =0.5x+50，

∴当x=130时， =0.5×130+50=115

【解析】（1）根据题意，计算分数在100﹣110内的频率，求出该班总人数，再计算分数在110﹣115内的频率，计算对应的人数；（2）求出分数6名学生中女生有2名，得出6名学生中选出3人，女生人数ξ的可能取值，再计算对应的概率值，写出ξ的分布列，计算数学期望值；（3）计算 、 ，求出回归系数 、写出对应线性回归方程，根据方程计算x=130时 的值即可．