
【题目】函数![]() 同时满足:①对于定义域上的任意
同时满足:①对于定义域上的任意![]() ,恒有
,恒有![]() ;②对于定义域上的任意
;②对于定义域上的任意![]() .当
.当![]() ,恒有
,恒有![]() .则称函数
.则称函数![]() 为“理想函数”,则下列三个函数中:
为“理想函数”,则下列三个函数中:
(1)![]() ,
,
(2)![]() ,
,
(3)![]() .
.
称为“理想函数”的有 (填序号)
科目:高中数学 来源: 题型:
【题目】已知过原点的动直线l与圆![]() 相交于不同的两点A,B.
相交于不同的两点A,B.
(1)求线段AB的中点M的轨迹C的方程;
(2)是否存在实数k,使得直线L:y=k(x﹣4)与曲线C只有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校某次N名学生的学科能力测评成绩(满分120分)的频率分布直方图如下,已知分数在100﹣110的学生数有21人
(1)求总人数N和分数在110﹣115分的人数n.;
(2)现准备从分数在110﹣115的n名学生(女生占 ![]() )中选3位分配给A老师进行指导,设随机变量ξ表示选出的3位学生中女生的人数,求ξ的分布列与数学期望Eξ;
)中选3位分配给A老师进行指导,设随机变量ξ表示选出的3位学生中女生的人数,求ξ的分布列与数学期望Eξ;
(3)为了分析某个学生的学习状态,对其下一阶段的学习提供指导建议,对他前7次考试的数学成绩x、物理成绩y进行分析,该生7次考试成绩如表
数学(x) | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理(y) | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩y与数学成绩x是线性相关的,求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() .若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
.若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据(x1 , y1),(x2 , y2),…,(xn , yn),其回归方程 ![]() =
= ![]() x+
x+ ![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ![]() =
= 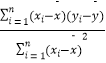 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学在“三关心”(即关心家庭、关心学校、关心社会)的专题中,对个税起征点问题进行了学习调查.学校决定从高一年级800人,高二年级1000人,高三年级800人中按分层抽样的方法共抽取13人进行谈话,其中认为个税起征点为3000元的有3人,认为个税起征点为4000元的有6人,认为个税起征点为 5000元的有4人.
(1)求高一年级、高二年级、高三年级分别抽取多少人?
(2)从13人中选出3人,求至少有1人认为个税起征点为4000元的概率;
(3)记从13人中选出3人中认为个税起征点为4000元的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差不为0的等差数列,首项a1=1,且a1 , a2 , a4成等比数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}满足bn=an+2 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 和
和![]() 在
在![]() 的图象如图所示:
的图象如图所示:
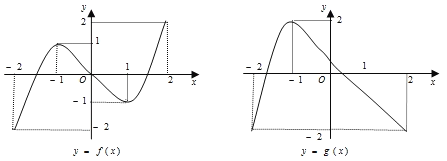
给出下列四个命题:
(1)方程![]() 有且仅有6个根;
有且仅有6个根;
(2)方程![]() 有且仅有3个根;
有且仅有3个根;
(3)方程![]() 有且仅有5个根;
有且仅有5个根;
(4)方程![]() 有且仅有4个根.
有且仅有4个根.
其中正确命题的个数是( )
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an},{bn}中,a1=2,b1=4且an , bn , an+1成等差数列,bn , an+1 , bn+1成等比数列(n∈N*)
(1)求a2 , a3 , a4及b2 , b3 , b4;由此归纳出{an},{bn}的通项公式,并证明你的结论.
(2)若cn=log2(![]() ),Sn=c1+c2+…+cn , 试问是否存在正整数m,使Sm≥5,若存在,求最小的正整数m.
),Sn=c1+c2+…+cn , 试问是否存在正整数m,使Sm≥5,若存在,求最小的正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , a1=1,且nan+1=2Sn(n∈N*),数列{bn}满足b1=![]() , b2=
, b2=![]() , 对任意n∈N* , 都有bn+12=bnbn+2 .
, 对任意n∈N* , 都有bn+12=bnbn+2 .
求数列{an}、{bn}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com