
【题目】已知函数![]() .
.
(1)设![]() 是函数
是函数![]() 的极值点,求
的极值点,求![]() 的值并讨论
的值并讨论![]() 的单调性;
的单调性;
(2)当![]() 时,证明:
时,证明:![]() >
>![]() .
.
【答案】(1)函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)见解析.
【解析】
试题(1)根据![]() 是
是![]() 的极值点得
的极值点得![]() ,可得导函数值为0,即
,可得导函数值为0,即![]() ,求得
,求得![]() .进一步讨论导函数为正、负的区间,即得解;
.进一步讨论导函数为正、负的区间,即得解;
(2)可以有两种思路,一种是注意到当![]() ,
,![]() 时,
时,![]() ,
,
转化成证明当![]() 时,
时,![]() >
>![]() .
.
研究函数当![]() 时,
时, ![]() 取得最小值且
取得最小值且![]() .
.
证得![]() ,
,![]() =
=![]()
![]() =
=![]()
![]()
![]() .
.
得证.
第二种思路是:当![]() ,
,![]() 时,
时,![]() ,根据
,根据![]() ,转化成
,转化成![]() .
.
构造函数![]()
![]() ,研究得到函数
,研究得到函数![]() 在
在![]() 时取唯一的极小值即最小值为
时取唯一的极小值即最小值为![]() .达到证明目的.
.达到证明目的.
试题解析:(1)![]() ,由
,由![]() 是
是![]() 的极值点得
的极值点得![]() ,
,
即![]() ,所以
,所以![]() . 2分
. 2分
于是![]() ,
,![]() ,
,
由![]() 知
知 ![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,
,
所以![]() 是
是![]() 的唯一零点. 4分
的唯一零点. 4分
因此,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,所以,函数
,所以,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增. 6分
上单调递增. 6分
(2)解法一:当![]() ,
,![]() 时,
时,![]() ,
,
故只需证明当![]() 时,
时,![]() >
>![]() . 8分
. 8分
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,
故![]() 在
在![]() 上有唯一实根
上有唯一实根![]() ,且
,且![]() . 10分
. 10分
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
从而当![]() 时,
时, ![]() 取得最小值且
取得最小值且![]() .
.
由![]() 得
得![]() ,
,![]() . 12分
. 12分
故![]()
![]() =
=![]()
![]() =
=![]()
![]()
![]() .
.
综上,当![]() 时,
时,![]()
![]() . 14分
. 14分
解法二:当![]() ,
,![]() 时,
时,![]() ,又
,又![]() ,所以
,所以
![]() . 8分
. 8分
取函数![]()
![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增,得函数
单调递增,得函数![]() 在
在![]() 时取唯一的极小值即最小值为
时取唯一的极小值即最小值为![]() . 12分
. 12分
所以![]() ,而上式三个不等号不能同时成立,故
,而上式三个不等号不能同时成立,故![]() >
>![]() . 14分
. 14分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() 满足:①圆心在第一象限,截
满足:①圆心在第一象限,截![]() 轴所得弦长为2;②被
轴所得弦长为2;②被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() ;③圆心到直线
;③圆心到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 分别做圆
分别做圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校高一1000名学生的物理成绩,随机抽查了部分学生的期中考试成绩,将数据整理后绘制成如图所示的频率分布直方图.
(1)估计该校高一学生物理成绩不低于80分的人数;
(2)若在本次考试中,规定物理成绩在m分以上(包括m分)的为优秀,该校学生物理成绩的优秀率大约为18%,求m的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出两块面积相同的正三角形纸片如图,要求用其中一块剪拼成一个正三棱锥(正三棱锥的三个侧面是全等的等腰三角形)模型,另一块剪拼成一个正三棱柱(正三棱柱上、下底面是正三角形,侧面是矩形)模型,使纸片正好用完,请设计一种剪拼方法,分别标示在图(1)(2)中,并作简要说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】身体素质拓展训练中,人从竖直墙壁的顶点A沿光滑杆自由下滑到倾斜的木板上(人可看作质点),若木板的倾斜角不同,人沿着三条不同路径AB、AC、AD滑到木板上的时间分别为t1、t2、t3,若已知AB、AC、AD与板的夹角分别为70o、90o和105o,则( )

A. t1>t2>t3 B. t1<t2<t3 C. t1=t2=t3 D. 不能确定t1、t2、t3之间的关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),┄,[80,90],并整理得到如下频率分布直方图:
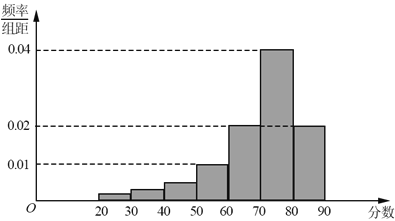
(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com