
已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上截距相等,求切线的方程;
(2)若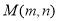 为圆C上任意一点,求
为圆C上任意一点,求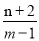 的最大值与最小值;
的最大值与最小值;
(3)从圆C外一点P(x,y)向圆引切线PM,M为切点,O为坐标原点,且有|PM|=|PO|,求当|PM|最小时的点P的坐标。
(1)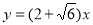 或
或 ;或
;或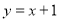 ,或
,或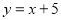 ;(2)最大值为-1,最小值为-7.;(3)当y=
;(2)最大值为-1,最小值为-7.;(3)当y=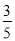 即P(
即P(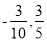 )时,|PM|最小.
)时,|PM|最小.
【解析】
试题分析:(1)当截距为0时,设出切线方程为y=kx,同理列出关于k的方程,求出方程的解即可得到k的值,得到切线的方程;当截距不为零时,根据圆C的切线在x轴和y轴的截距相等,设出切线方程x+y=b,然后利用点到直线的距离公式求出圆心到切线的距离d,让d等于圆的半径r,列出关于b的方程,求出方程的解即可得到b的值,得到切线的方程; (2)设 ,则
,则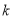 表示直线MA的斜率;其中A(1,-2)是定点;因为
表示直线MA的斜率;其中A(1,-2)是定点;因为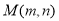 在圆C上,所以圆C与直线MA有公共点,而直线MA方程为:y+2=
在圆C上,所以圆C与直线MA有公共点,而直线MA方程为:y+2= (x-1),则有:C点到直线MA的距离不大于圆C的半径,即:
(x-1),则有:C点到直线MA的距离不大于圆C的半径,即: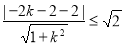 ,解得:
,解得: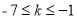 ,即可求出
,即可求出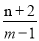 的最大值为和最小值;(3)根据圆切线垂直于过切点的半径,得到三角形CPM为直角三角形,根据勾股定理表示出点P的轨迹方程,由轨迹方程得到动点P的轨迹为一条直线,所以|PM|的最小值就是|PO|的最小值,求出原点到P轨迹方程的距离即为|PO|的最小值,然后利用两点间的距离公式表示出P到O的距离,把P代入动点的轨迹方程,两者联立即可此时P的坐标.
的最大值为和最小值;(3)根据圆切线垂直于过切点的半径,得到三角形CPM为直角三角形,根据勾股定理表示出点P的轨迹方程,由轨迹方程得到动点P的轨迹为一条直线,所以|PM|的最小值就是|PO|的最小值,求出原点到P轨迹方程的距离即为|PO|的最小值,然后利用两点间的距离公式表示出P到O的距离,把P代入动点的轨迹方程,两者联立即可此时P的坐标.
【解析】
圆C的方程为:(x+1)2+(y-2)2=2
(1)圆C的切线在x轴和y轴上截距相等时,切线过原点或切线的斜率为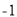 ;
;
当切线过原点时,设切线方程为:y=kx,相切则: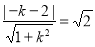 ,得
,得 ;
;
当切线的斜率为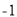 时,设切线方程为:y=-x+b,由相切得:
时,设切线方程为:y=-x+b,由相切得: ,
,
得b=1或b=5;故所求切线方程为: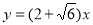 或
或 ;或
;或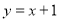 ,或
,或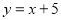
(2)设 ,则
,则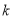 表示直线MA的斜率;其中A(1,-2)是定点;
表示直线MA的斜率;其中A(1,-2)是定点;
因为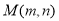 在圆C上,所以圆C与直线MA有公共点,
在圆C上,所以圆C与直线MA有公共点,
而直线MA方程为:y+2= (x-1),则有:C点到直线MA的距离不大于圆C的半径
(x-1),则有:C点到直线MA的距离不大于圆C的半径
即: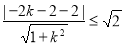 ,解得:
,解得: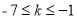 ,即
,即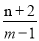 的最大值为-1,最小值为-7.
的最大值为-1,最小值为-7.
(3)由圆的切线长公式得|PM|2=|PC|2-R2=(x+1)2+(y-2)2-2;
由|PM|=|PO|得:(x+1)2+(y-2)2-2=x2+y2;即2x-4y+3=0, 即x=2y-
此时|PM|=|PO|=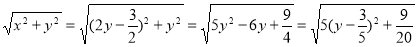
所以当y=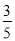 即P(
即P(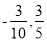 )时,|PM|最小.
)时,|PM|最小.
考点:1.直线的方程;2.直线与圆的位置关系.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016届陕西省高一下学期期中考试数学试卷(解析版) 题型:选择题
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到300度之间,频率分布直方图所示,则在这些用户中,用电量落在区间 内的户数为( )
内的户数为( )

A. B.
B. C.
C.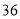 D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届陕西省安康市高一上学期期末质量检测数学试卷(解析版) 题型:选择题
与圆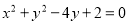 相切,并在
相切,并在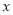 轴、
轴、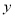 轴上的截距相等的直线共有( )
轴上的截距相等的直线共有( )
A.6条 B.5条 C.4条 D.3条
查看答案和解析>>
科目:高中数学 来源:2016届陕西省安康市高一上学期期末质量检测数学试卷(解析版) 题型:选择题
已知指数函数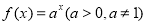 ,且过点(2,4),
,且过点(2,4),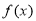 的反函数记为
的反函数记为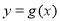 ,则
,则 的解析式是:( )
的解析式是:( )
A.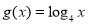 B.
B.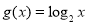 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届陕西省高一下学期期中考试数学试卷(解析版) 题型:解答题
根据以下算法的程序,画出其相应的算法程图,并指明该算法的目的及输出结果.
n=1
S=0
Do
S=S+n
n=n+1
Loop while S 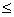 2010
2010
输出n-1
查看答案和解析>>
科目:高中数学 来源:2016届陕西省高一下学期期中考试数学试卷(解析版) 题型:选择题
向如图中所示正方形内随机地投掷飞镖,飞镖落在阴影部分的概率为 ( ).
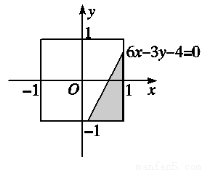
A.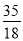 B.
B.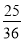 C.
C.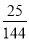 D.
D.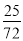
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com