
【题目】设![]() 、
、![]() 是椭圆
是椭圆![]() 的左、右顶点,
的左、右顶点,![]() 为椭圆上异于
为椭圆上异于![]() 、
、![]() 的一点.
的一点.
(1)![]() 是椭圆
是椭圆![]() 的上顶点,且直线
的上顶点,且直线![]() 与直线
与直线![]() 垂直,求点
垂直,求点![]() 到
到![]() 轴的距离;
轴的距离;
(2)过点![]() 的直线
的直线![]() (不过坐标原点)与椭圆
(不过坐标原点)与椭圆![]() 交于
交于![]() 、
、![]() 两点,且点
两点,且点![]() 在
在![]() 轴上方,点
轴上方,点![]() 在
在![]() 轴下方,若
轴下方,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(wx+![]() )(w>0,
)(w>0,![]() <
<![]() )的最小正周期是π,若将该函数的图象向右平移
)的最小正周期是π,若将该函数的图象向右平移![]() 个单位后得到的函数图象关于直线x=
个单位后得到的函数图象关于直线x=![]() 对称,则函数f(x)的解析式为( )
对称,则函数f(x)的解析式为( )
A.f(x)=sin(2x+![]() )B.f(x)=sin(2x-
)B.f(x)=sin(2x-![]() )
)
C.f(x)=sin(2x+![]() )D.f(x)=sin(2x-
)D.f(x)=sin(2x-![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年末,武汉出现新型冠状病毒肺炎(![]() )疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,所以目前没有特异治疗方法,防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,一户6口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为
)疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,所以目前没有特异治疗方法,防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,一户6口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为![]() (
(![]() )且相互独立,该家庭至少检测了5个人才能确定为“感染高危户”的概率为
)且相互独立,该家庭至少检测了5个人才能确定为“感染高危户”的概率为![]() ,当
,当![]() 时,
时,![]() 最大,则
最大,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中点,点
中点,点![]() 在线段
在线段![]() 上.
上.
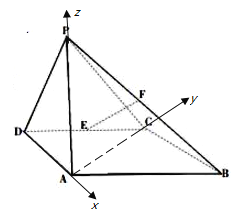
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]()
![]()
![]()
![]() ,求实数
,求实数![]() 使直线
使直线![]() 与平面
与平面![]() 所成角和直线
所成角和直线![]() 与平面
与平面![]() 所成角相等.
所成角相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第7届世界军人运动会于2019年10月18日至27日在湖北武汉举行,赛期10天,共设置射击、游泳、田径、篮球等27个大项,329个小项.共有来自100多个国家的近万名现役军人同台竞技.前期为迎接军运会顺利召开,武汉市很多单位和部门都开展了丰富多彩的宣传和教育活动,努力让大家更多的了解军运会的相关知识,并倡议大家做文明公民.武汉市体育局为了解广大民众对军运会知识的知晓情况,在全市开展了网上问卷调查,民众参与度极高,现从大批参与者中随机抽取200名幸运参与者,他们得分(满分100分)数据,统计结果如下:
组别 |
|
|
|
|
|
|
|
频数 | 5 | 30 | 40 | 50 | 45 | 20 | 10 |
(1)若此次问卷调查得分整体服从正态分布,用样本来估计总体,设![]() ,
,![]() 分别为这200人得分的平均值和标准差(同一组数据用该区间中点值作为代表),求
分别为这200人得分的平均值和标准差(同一组数据用该区间中点值作为代表),求![]() ,
,![]() 的值(
的值(![]() ,
,![]() 的值四舍五入取整数),并计算
的值四舍五入取整数),并计算![]() ;
;
(2)在(1)的条件下,为感谢大家参与这次活动,市体育局还对参加问卷调查的幸运市民制定如下奖励方案:得分低于![]() 的可以获得1次抽奖机会,得分不低于
的可以获得1次抽奖机会,得分不低于![]() 的可获得2次抽奖机会,在一次抽奖中,抽中价值为15元的纪念品A的概率为
的可获得2次抽奖机会,在一次抽奖中,抽中价值为15元的纪念品A的概率为![]() ,抽中价值为30元的纪念品B的概率为
,抽中价值为30元的纪念品B的概率为![]() .现有市民张先生参加了此次问卷调查并成为幸运参与者,记Y为他参加活动获得纪念品的总价值,求Y的分布列和数学期望,并估算此次纪念品所需要的总金额.
.现有市民张先生参加了此次问卷调查并成为幸运参与者,记Y为他参加活动获得纪念品的总价值,求Y的分布列和数学期望,并估算此次纪念品所需要的总金额.
(参考数据:![]() ;
;![]() ;
;![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴不重合,交圆
轴不重合,交圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)求![]() 的值;
的值;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 相交于
相交于![]() 点,试问在椭圆
点,试问在椭圆![]() 上是否存在一定点
上是否存在一定点![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列(其中
成等差数列(其中![]() ,
,![]() ,
,![]() 分别指直线
分别指直线![]() ,
,![]() ,
,![]() 的斜率).若存在,求出
的斜率).若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与
与![]() ,
,![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() ,若点
,若点![]() 在曲线
在曲线![]() 位于第一象限的图象上运动,求四边形
位于第一象限的图象上运动,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)试讨论函数![]() 的极值点的个数;
的极值点的个数;
(2)若![]() ,且
,且![]() 恒成立,求a的最大值.
恒成立,求a的最大值.
参考数据:
| 1.6 | 1.7 | 1.74 | 1.8 | 10 |
| 4.953 | 5.474 | 5.697 | 6.050 | 22026 |
| 0.470 | 0.531 | 0.554 | 0.588 | 2.303 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com