
【题目】已知f(x)= ![]() ,g(x)=ax3﹣x2﹣x+b(a,b∈R,a≠0),g(x)的图象C在x=﹣
,g(x)=ax3﹣x2﹣x+b(a,b∈R,a≠0),g(x)的图象C在x=﹣ ![]() 处的切线方程是y=
处的切线方程是y= ![]() .
.
(1)若求a,b的值,并证明:当x∈(﹣∞,2]时,g(x)的图象C上任意一点都在切线y= ![]() 上或在其下方;
上或在其下方;
(2)求证:当x∈(﹣∞,2]时,f(x)≥g(x).
【答案】
(1)解:g'(x)=3ax2﹣2x﹣1,
因为g(x)=ax3﹣x2﹣x+b的图象C在 ![]() 处的切线方程是
处的切线方程是 ![]() ,
,
所以 ![]() ,即
,即 ![]() ,解得a=1.
,解得a=1.
因为图象C过点 ![]() ,所以
,所以 ![]() ,解得
,解得 ![]() .
.
要证明:当x∈(﹣∞,2]时,g(x)的图象C上任意一点都在切线 ![]() 上或在其下方,
上或在其下方,
只要证明:当x∈(﹣∞,2]时, ![]() .
.
令 ![]() ,
,
![]() ,令
,令 ![]() ,得
,得 ![]() ,
,
验证得 ![]() ,
,
所以x∈(﹣∞,2], ![]() 成立,
成立,
所以当x∈(﹣∞,2]时,g(x)的图象C上任意一点都在切线 ![]() 上或在其下方
上或在其下方
(2)解:只要证明:x∈(﹣∞,2], ![]() .
.
x∈(﹣∞,2],令 ![]() ,
,
![]() ,令
,令 ![]() ,
,
当 ![]() 时,h'(x)<0,当
时,h'(x)<0,当 ![]() 时,h'(x)>0,所以
时,h'(x)>0,所以 ![]() ,
,
所以x∈(﹣∞,2], ![]() 成立,
成立,
又由(1)得,x∈(﹣∞,2], ![]() ,
,
所以x∈(﹣∞,2], ![]() ,
,
所以x∈(﹣∞,2],f(x)≥g(x).
【解析】(1)求出函数的导数,根据 ![]() ,求出a的值,图象C过点
,求出a的值,图象C过点 ![]() ,求出b的值,问题转化为证明当x∈(﹣∞,2]时,
,求出b的值,问题转化为证明当x∈(﹣∞,2]时, ![]() ,根据函数的单调性证明即可;(2)问题转化为证明x∈(﹣∞,2],
,根据函数的单调性证明即可;(2)问题转化为证明x∈(﹣∞,2], ![]() ,构造函数g(x),根据函数的单调性证明即可.
,构造函数g(x),根据函数的单调性证明即可.
【考点精析】认真审题,首先需要了解函数的最大(小)值与导数(求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值).
比较,其中最大的是一个最大值,最小的是最小值).


科目:高中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)函数在区间[﹣1,1]上的最小值记为![]() ,求
,求![]() 的解析式;
的解析式;
(2)求(1)中![]() 的最大值;
的最大值;
(3)若函数![]() 在[2,4]上是单调增函数,求实数
在[2,4]上是单调增函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x),满足当x>0时,f(x)>1,且对任意的x,y![]() ,有
,有![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)求证:对任意x![]() ,都有f(x)>0;
,都有f(x)>0;
(3)解不等式f(3![]() 2x)>4.
2x)>4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于某产品的明星代言费x(百万元)和其销售额y(百万元),有如表的统计表格:
i | 1 | 2 | 3 | 4 | 5 | 合计 |
xi(百万元) | 1.26 | 1.44 | 1.59 | 1.71 | 1.82 | 7.82 |
wi(百万元) | 2.00 | 2.99 | 4.02 | 5.00 | 6.03 | 20.04 |
yi(百万元) | 3.20 | 4.80 | 6.50 | 7.50 | 8.00 | 30.00 |
| ||||||
其中 ![]() .
.
(1)在坐标系中,作出销售额y关于广告费x的回归方程的散点图,根据散点图指出:y=a+blnx,y=c+dx3哪一个适合作销售额y关于明星代言费x的回归类方程(不需要说明理由); 
(2)已知这种产品的纯收益z(百万元)与x,y有如下关系:x=0.2y﹣0.726x(x∈[1.00,2.00]),试写出z=f(x)的函数关系式,试估计当x取何值时,纯收益z取最大值?(以上计算过程中的数据统一保留到小数点第2位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知AB是⊙O的直径,直线AF交⊙O于F(不与B重合),直线EC与⊙O相切于C,交AB于E,连接AC,且∠OAC=∠CAF,求证: 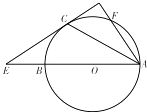
(1)AF⊥EC;
(2)若AE=5,AF=2,求AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xoy中,直线l的参数方程是  (t为参数),以射线ox为极轴建立极坐标系,曲线C的极坐标方程是
(t为参数),以射线ox为极轴建立极坐标系,曲线C的极坐标方程是 ![]() +ρ2sin2θ=1.
+ρ2sin2θ=1.
(1)求曲线C的直角坐标方程;
(2)求直线l与曲线C相交所得的弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】①在同一坐标系中,![]() 与
与![]() 的图象关于
的图象关于![]() 轴对称;
轴对称;
②![]() 是奇函数;
是奇函数;
③![]() 的图象关于
的图象关于![]() 成中心对称;
成中心对称;
④![]() 的最大值为
的最大值为![]() ;
;
⑤![]() 的单调增区间:
的单调增区间:![]() 。
。
以上五个判断正确有____________________(写上所有正确判断的序号)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,-2),椭圆E: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为![]() ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的动直线l与E相交于P,Q两点.当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com