
【题目】已知二次函数![]() .
.
(1)函数在区间[﹣1,1]上的最小值记为![]() ,求
,求![]() 的解析式;
的解析式;
(2)求(1)中![]() 的最大值;
的最大值;
(3)若函数![]() 在[2,4]上是单调增函数,求实数
在[2,4]上是单调增函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)0(3)m≤3或m≥8
【解析】
(1)根据对称轴与定义区间位置关系,分类求解最小值,按分段函数形式写![]() 的解析式;(2)根据一次函数与二次函数性质分段讨论函数最大值,最后取最大值中最大值,(3)先转化:f(x)在[2,4]上单调递增且恒非负,或单调递减且恒非正,再根据对称轴以及单调性列方程组,解得实数
的解析式;(2)根据一次函数与二次函数性质分段讨论函数最大值,最后取最大值中最大值,(3)先转化:f(x)在[2,4]上单调递增且恒非负,或单调递减且恒非正,再根据对称轴以及单调性列方程组,解得实数![]() 的取值范围.
的取值范围.
解:(1)f(x)=x2﹣mx+m﹣1=![]() ,对称轴为x=
,对称轴为x=![]() .
.
①若![]() ,此时函数f(x)在区间[﹣1,1]上单调递增,所以最小值g(m)=f(﹣1)=2m.
,此时函数f(x)在区间[﹣1,1]上单调递增,所以最小值g(m)=f(﹣1)=2m.
②若![]() ,此时当x=
,此时当x=![]() 时,函数f(x)最小,最小值g(m)=f(
时,函数f(x)最小,最小值g(m)=f(![]() )=
)=![]() .
.
③若![]() ,此时函数f(x)在区间[﹣1,1]上单调递减,所以最小值g(m)=f(1)=0.
,此时函数f(x)在区间[﹣1,1]上单调递减,所以最小值g(m)=f(1)=0.
综上g(m)=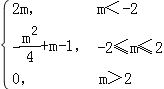 .
.
(2)由(1)知g(m)=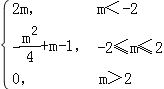 .
.
当m<﹣2时,g(m)=2m<﹣4,
当﹣2≤m≤2,g(m)=![]() =
=![]()
当m>2时,g(m)=0.
综上g(m)的最大值为0.
(3)要使函数y=|f(x)|在[2,4]上是单调增函数,则f(x)在[2,4]上单调递增且恒非负,或单调递减且恒非正,
∴ ,
,
所以![]() 或
或![]() ,
,
解得m≤3或m≥8.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】如图,在△ABC和△ACD中,∠ACB=∠ADC=90°,∠BAC=∠CAD,⊙O是以AB为直径的圆,DC的延长线与AB的延长线交于点E.
(Ⅰ)求证:DC是⊙O的切线;
(Ⅱ)若EB=6,EC=6 ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的数列{an}的前n项和Sn>1,且6Sn=(an+1)(an+2),n∈N* .
(1)求{an}的通项公式;
(2)若数列{bn}满足bn= ![]() ,求{bn}的前n项和.
,求{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是⊙O的一条切线,切点为B,直线ADE、CFD、CGE都是⊙O的割线,已知AC=AB. 
(1)若CG=1,CD=4.求 ![]() 的值.
的值.
(2)求证:FG∥AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在![]() 上的函数
上的函数![]() 对于任意实数
对于任意实数![]() ,都有
,都有![]() 成立,且
成立,且![]() ,当
,当![]() 时,
时,![]() .
.
(1)判断![]() 的单调性,并加以证明;
的单调性,并加以证明;
(2)试问:当![]() 时,
时,![]() 是否有最值?如果有,求出最值;如果没有,说明理由;
是否有最值?如果有,求出最值;如果没有,说明理由;
(3)解关于![]() 的不等式
的不等式![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学对男女学生是否喜爱古典音乐进行了一个调查,调查者对学校高三年级随机抽取了100名学生,调查结果如表:
喜爱 | 不喜爱 | 总计 | |
男学生 | 60 | 80 | |
女学生 | |||
总计 | 70 | 30 |
附:K2= ![]()
P(K2≥k0) | 0.100 | 0.050 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
(1)完成如表,并根据表中数据,判断是否有95%的把握认为“男学生和女学生喜欢古典音乐的程度有差异”;
(2)从以上被调查的学生中以性别为依据采用分层抽样的方式抽取10名学生,再从这10名学生中随机抽取5名学生去某古典音乐会的现场观看演出,求正好有X个男生去观看演出的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点.
(1)求圆A的方程;
(2)当|MN|=2![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构在某一学校随机抽取30名学生参加环保知识测试,测试成绩(单位:分)如图所示,假设得分值的中位数为me , 众数为m0 , 平均值为 ![]() ,则( )
,则( ) 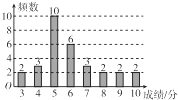
A.me=m0= ![]()
B.me=m0< ![]()
C.me<m0< ![]()
D.m0<me< ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() ,g(x)=ax3﹣x2﹣x+b(a,b∈R,a≠0),g(x)的图象C在x=﹣
,g(x)=ax3﹣x2﹣x+b(a,b∈R,a≠0),g(x)的图象C在x=﹣ ![]() 处的切线方程是y=
处的切线方程是y= ![]() .
.
(1)若求a,b的值,并证明:当x∈(﹣∞,2]时,g(x)的图象C上任意一点都在切线y= ![]() 上或在其下方;
上或在其下方;
(2)求证:当x∈(﹣∞,2]时,f(x)≥g(x).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com